Teste t e Teste z: Quando e Por Que Optar por Cada Um?
Os testes t e z são metodologias de inferência estatística empregadas para verificar a existência de diferenças significativas entre as médias de dois grupos ou populações. O teste t é recomendado para amostras menores ou quando a variância populacional é desconhecida; já o teste z é apropriado para grandes amostras, com variância populacional conhecida.
Introdução
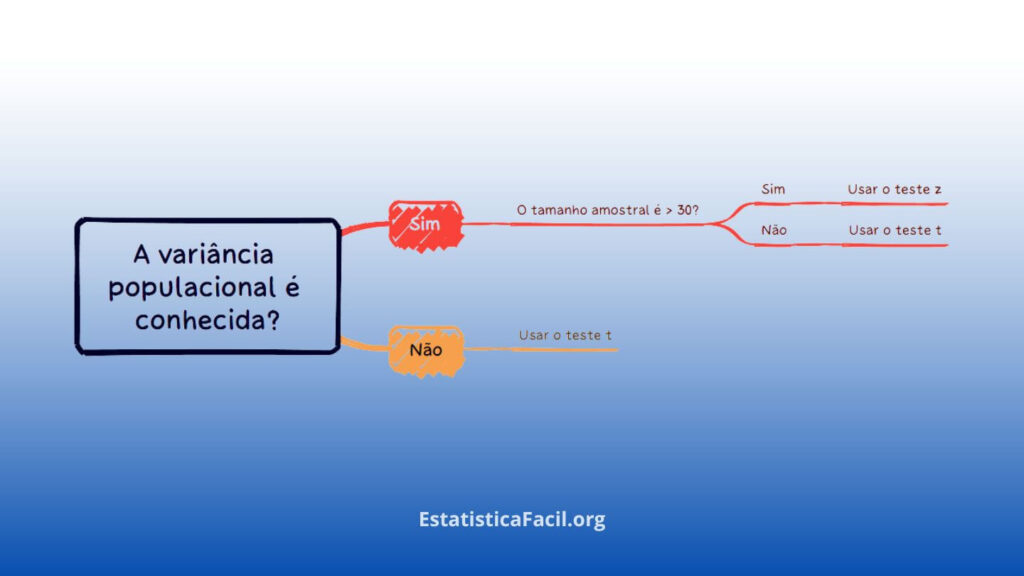
Na prática da análise de dados, a escolha correta entre o teste t e o teste z é fundamental para a obtenção de resultados precisos e confiáveis. Esses testes são ferramentas de hipóteses estatísticas projetadas para avaliar se há uma diferença marcante entre as médias de dois conjuntos distintos de dados. O teste t é utilizado em situações onde a variância populacional não é conhecida ou quando se lida com amostras de tamanho reduzido (n < 30). Por outro lado, o teste z é indicado quando se conhece a variância populacional (σ²) e o volume de dados é considerável (n > 30). Compreender o momento apropriado para usar cada teste e a importância dessa escolha são essenciais para assegurar a validade das análises realizadas e para fomentar decisões baseadas em evidências.
Destaques do Artigo
- O teste-t é indicado para casos em que a variância da população é desconhecida ou quando a amostra é limitada (n < 30).
- O teste-z é recomendado para situações onde a variância populacional é conhecida e o tamanho da amostra é amplo (n > 30).
- Dada a raridade em se conhecer com exatidão a variância populacional, o teste-z é aplicado com menos frequência.
- O teste-t utiliza a distribuição t de Student, caracterizada por suas caudas mais pesadas, ideal para amostras menores.
- O teste-z emprega a distribuição normal padrão, mais adequada para grandes amostras.
- Ambos os testes dependem da independência das observações e da normalidade dos dados ou resíduos, fundamentais para a validade dos resultados.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Premissas do Testes t e Teste z
Os testes t e z são ferramentas de inferência estatística projetadas para avaliar se há uma diferença significativa entre as médias de dois grupos ou populações distintas.
Para garantir a aplicação precisa desses testes, é fundamental assegurar a independência das observações. Isto é, os resultados de uma observação não devem influenciar os de outra, mantendo a integridade dos dados analisados.
A premissa de normalidade dos dados ou dos resíduos é essencial, indicando que estes devem se distribuir de maneira normal. Esse pressuposto é vital para a validação estatística dos resultados obtidos tanto pelo teste t quanto pelo teste z.
Além disso, outro pressuposto fundamental para a aplicação eficaz tanto do teste t quanto do teste z é a homocedasticidade, ou seja, a igualdade das variâncias entre os grupos comparados. Esse requisito é crucial porque diferenças significativas nas variâncias podem levar a conclusões errôneas sobre as diferenças entre as médias. A homocedasticidade garante que a variabilidade nos dados é uniforme em todos os grupos, proporcionando uma base sólida para a comparação das médias e a validade dos resultados dos testes.
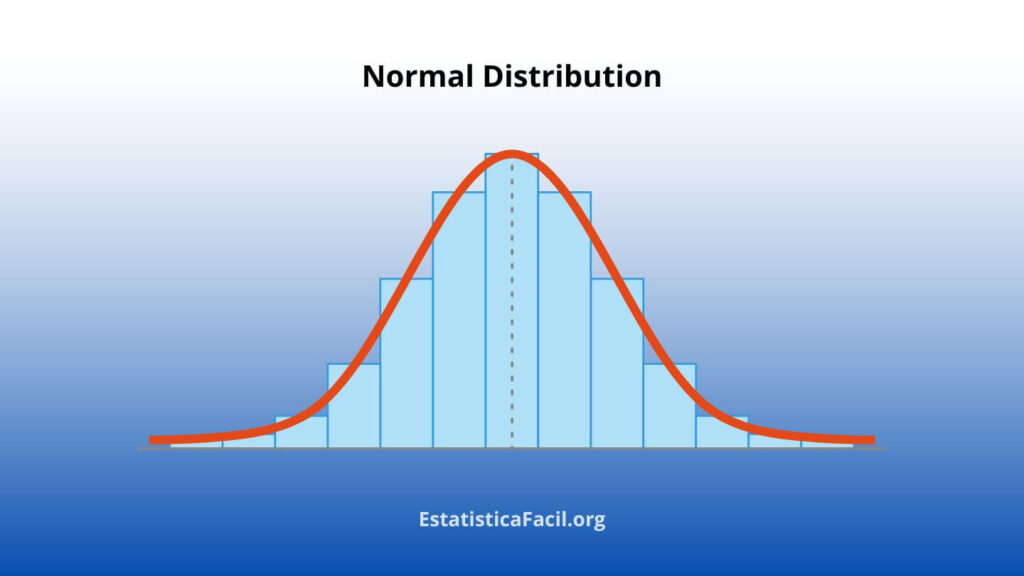
Distribuição Utilizada no Teste t e Teste z
O teste t utiliza a distribuição t de Student, conhecida por sua flexibilidade e caudas mais pesadas, o que a torna adequada para amostras menores e situações em que a variância populacional é desconhecida.
Com o aumento do tamanho da amostra, a distribuição t tende a se aproximar da distribuição normal padrão, que é empregada pelo teste z. Esta convergência é crucial para entender a transição entre o uso do teste t e o teste z em análises de dados.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Conclusão
A seleção criteriosa entre o teste t e o teste z é crucial para assegurar a precisão analítica em estudos estatísticos. Levando em consideração os pressupostos e as características dos dados em questão, é possível tomar decisões informadas sobre o teste mais adequado a ser utilizado.
Segue um guia prático para auxiliar na escolha do teste apropriado:
1. Opte pelo teste t se a variância da população for desconhecida ou se o tamanho da amostra for pequeno (n < 30). Este teste é particularmente vantajoso em cenários com limitações de dados e incerteza quanto à variância populacional, devido à sua distribuição t de Student.
2. Prefira o teste z quando a variância da população for conhecida e o tamanho da amostra for considerável (n > 30). Este teste se baseia na distribuição normal padrão, adequada para contextos em que as informações sobre a variância são claras e o volume de dados é substancial.
| Teste t | Teste z | |
|---|---|---|
| Variância populacional | Desconhecida | Conhecida |
| Tamanho da amostra | Pequena (n < 30) | Grande (n > 30) |
| Distribuição | Distribuição t de Student | Distribuição normal padrão |
| Pressupostos | Independência das observações, normalidade e homocedasticidade | Independência das observações, normalidade |
| Aplicabilidade | Dados limitados ou variância populacional desconhecida | Variância populacional conhecida e tamanho grande da amostra |
Note que o teste z não é comumente utilizado, pois é raro ter conhecimento da variância populacional, o que é quase impossível na maioria dos cenários.
Leitura Recomendada
Deseja ampliar seus conhecimentos? Explore nosso blog para descobrir mais artigos pertinentes e aprofunde seu entendimento dos testes estatísticos fundamentais. Aproveite essa chance para desenvolver suas habilidades em análise de dados e promover decisões mais embasadas. Acesse agora mesmo!
- Teste t: Não Ignore Esses Segredos
- O Desvio Padrão Pode Ser Negativo?
- O que é Estatística t, Teste t e Distribuição t?
- Tamanho Amostral Para o Teste t: Como Calcular?
- Como Reportar Corretamente os Resultados do Teste-t?
- T-test vs Z-test: When to Use Each Test and Why It Matters (Link Externo)
Perguntas Frequentes: Teste t e Teste z
O teste t é utilizado para comparar as médias de dois grupos quando a variância da população é desconhecida e o tamanho da amostra é reduzido (n < 30).
O teste z é aplicado na comparação das médias de dois grupos, idealmente quando a variância da população é conhecida e o tamanho da amostra é substancial (n > 30).
Para ambos os testes, é imprescindível a independência das observações e a normalidade e homocedasticidade dos dados ou resíduos, assegurando a integridade dos resultados analíticos.
O teste t utiliza a distribuição t de Student, adequada para amostras menores e variâncias populacionais desconhecidas.
O teste z emprega a distribuição normal padrão, ideal para grandes amostras com variância conhecida.
Com o aumento do tamanho da amostra, a distribuição t de Student gradativamente aproxima-se da distribuição normal padrão, ajustando-se ao contexto da análise.
A seleção correta do teste é fundamental para garantir a precisão dos resultados analíticos, conferindo confiabilidade às decisões baseadas em dados.
O teste t deve ser escolhido quando não se conhece a variância da população ou quando se trabalha com amostras pequenas (n < 30).
Sim, o teste oferece a variante específica para análise de dados pareados, o teste t para amostras pareadas.
Não, os testes t e z são projetados apenas para a comparação entre dois grupos. Para análises envolvendo mais grupos, é recomendado o uso de outros métodos, como a ANOVA (Análise de Variância).








