O que é Análise de Regressão? Um Guia Completo para Iniciantes
A análise de regressão é uma técnica estatística utilizada para modelar a relação entre a variável dependente e uma ou mais variáveis independentes, possibilitando previsões, tomadas de decisão e insights em diversos campos.
Introdução
A análise de regressão é uma técnica estatística que fornece insights significativos ao modelar as relações entre variáveis dependente e independentes, possibilitando previsões precisas e tomadas de decisão informadas em diversos campos profissionais. Ao empregar diferentes tipos de regressão, como linear, logística e polinomial, esta ferramenta versátil se adapta a várias estruturas de dados e objetivos analíticos. Desde a avaliação do impacto de políticas econômicas até a previsão de comportamentos de consumo e resultados de saúde, a análise de regressão destaca-se como fundamental para traduzir dados complexos em ações estratégicas e operacionais concretas.
Pontos-chave
- A análise de regressão modela relações entre variáveis dependentes e independentes para previsão e tomada de decisão.
- Linear, logística e polinomial são os principais tipos de regressão, cada um adequado a diferentes dados e objetivos.
- Métricas de ajuste, como R-quadrado e R-quadrado ajustado, avaliam o desempenho e a explicabilidade do modelo.
- As suposições de regressão incluem linearidade, normalidade, independência dos erros e homocedasticidade, que devem ser validadas.
- Armadilhas comuns incluem confundir correlação com causalidade, sobreajuste, multicolinearidade, viés de variável omitida e extrapolação.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
O que é análise de regressão?
A análise de regressão é uma técnica fundamental em estatística e ciência de dados que nos permite explorar e quantificar as relações entre variáveis. É utilizada para prever resultados, identificar tendências e tomar decisões baseadas em dados em diversos campos, desde negócios e finanças até saúde e engenharia.
Em sua essência, a análise de regressão busca modelar a relação entre uma variável dependente (a variável que estamos tentando prever ou explicar) e uma ou mais variáveis independentes (os fatores que influenciam a variável dependente). Ao fazer isso, podemos obter insights sobre os padrões subjacentes e as relações causais dos nossos dados, o que nos permite fazer previsões melhores e tomar decisões mais informadas.
A ideia fundamental por trás da análise de regressão é encontrar o modelo mais adequado que represente com precisão a relação entre as variáveis dependente e independente(s). Isso geralmente envolve ajustar uma linha ou curva aos pontos de dados para minimizar as diferenças entre os valores observados e previstos, conhecidas como resíduos.
Na prática, a análise de regressão pode assumir muitas formas, desde a regressão linear simples, que modela a relação entre uma variável dependente e uma independente, até técnicas mais avançadas, como a regressão polinomial múltipla, que permite a análise de relações mais complexas.
Como uma ferramenta estatística versátil e poderosa, a análise de regressão é essencial para qualquer um que deseje compreender dados e tirar conclusões. Neste guia, você aprenderá sobre os diversos tipos de análise de regressão, seus conceitos fundamentais, premissas, limitações e aplicações. Ao entender o que é análise de regressão e dominar essa técnica, você estará bem preparado para enfrentar desafios complexos envolvendo dados e tomar decisões mais acertadas.
Tipos de Análise de Regressão
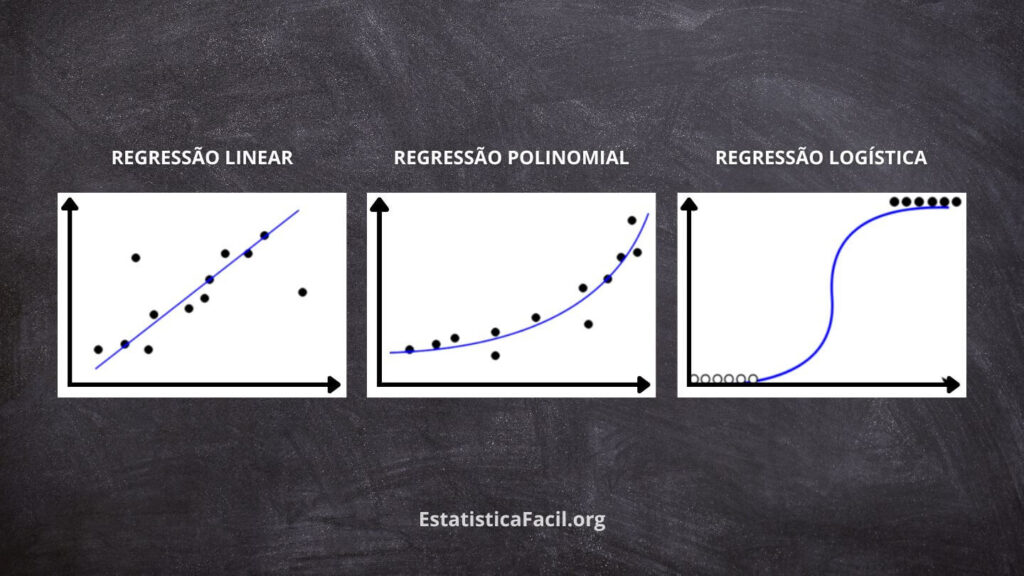
Regressão Linear: Esta é a forma mais básica de análise de regressão para modelar a relação entre as variáveis dependente e independente(s). Assume-se uma relação linear entre as variáveis, representada por uma linha reta. O objetivo é encontrar a linha que melhor se ajusta, minimizando a soma dos quadrados das diferenças entre os valores observados e previstos. A regressão linear é amplamente utilizada para previsões, análise de tendências e identificação do impacto de uma variável sobre outra.
Regressão Logística: Este tipo de análise de regressão é projetado para problemas com variáveis dependentes categóricas, incluindo binária (dois possíveis resultados), nominal (categorias não ordenadas) e ordinal (categorias ordenadas). Em vez de prever o valor real da variável dependente, a regressão logística estima a probabilidade de ocorrência de um evento com base na variável independente. Utiliza a função logística, que transforma a saída do modelo de regressão em um valor de probabilidade entre 0 e 1. Comumente usada em campos como pesquisa médica, marketing e finanças, a regressão logística é versátil para prever a probabilidade de eventos ou resultados específicos e entender o impacto de vários fatores sobre esses resultados.
Regressão Polinomial: Esta é uma extensão da regressão linear usada quando a relação entre as variáveis dependentes e independentes não é linear. Em vez de ajustar uma linha reta, uma função polinomial é usada para modelar a curvatura na relação. A regressão polinomial pode capturar padrões mais complexos nos dados, proporcionando um ajuste melhor para situações onde modelos lineares são inadequados. No entanto, é essencial ter cautela com a escolha dos graus polinomiais, pois modelos excessivamente complexos podem levar ao sobreajuste e à má generalização de novos dados.
Regressão Múltipla: A regressão múltipla é uma técnica avançada que permite a inclusão de múltiplas variáveis independentes, possibilitando a análise de relações mais complexas entre as variáveis e o controle de fatores confundidores. Não é apenas uma generalização da regressão linear, mas também pode ser estendida para outros tipos de regressão, como logística e polinomial. A regressão múltipla visa encontrar o modelo que melhor explica a relação entre variáveis dependente e independentes.
Conceitos Fundamentais da Análise de Regressão
Variáveis Dependente e Independente: Na análise de regressão, a variável dependente (ou variável resposta) é o resultado que tentamos prever ou explicar, a que sofre o efeito; enquanto a variável independente (ou variável preditora ou explicativa) representa o fator que influencia a variável dependente, a que causa o efeito. A análise de regressão visa modelar a relação entre essas variáveis, permitindo-nos entender os efeitos das variáveis independentes sobre a variável dependente e fazer previsões.
Coeficientes e Interceptos: Coeficientes e interceptos são componentes essenciais de um modelo de regressão. Os coeficientes representam o efeito das variáveis independentes sobre a variável dependente, indicando quanto a variável dependente muda para cada aumento unitário nas variáveis independentes, assumindo que todas as outras variáveis se mantêm constantes. O intercepto representa o valor esperado da variável dependente quando todas as variáveis independentes são iguais a zero. Esses valores são estimados usando técnicas de mínimos quadrados ordinários ou de máxima verossimilhança durante o ajuste do modelo.
Adequação do Modelo e R-quadrado: A adequação do modelo mede quão bem o modelo de regressão se ajusta aos dados observados. Várias métricas podem ser usadas para avaliar a adequação, mas uma das mais comuns é o R-quadrado (também conhecido como coeficiente de determinação). O R-quadrado representa a proporção da variância na variável dependente explicada pelas variáveis independentes do modelo. Ele varia entre 0 e 1, com valores mais altos indicando um melhor ajuste.
Na regressão múltipla, é essencial considerar o R-quadrado ajustado, que leva em conta o número de variáveis independentes no modelo. O valor de R-quadrado pode aumentar à medida que mais variáveis são adicionadas, mesmo que as variáveis adicionais não contribuam significativamente para o poder preditivo do modelo. O R-quadrado ajustado corrige esse problema penalizando o valor de R-quadrado pela inclusão de variáveis desnecessárias. Isso resulta em uma avaliação mais precisa do desempenho do modelo e ajuda a prevenir o sobreajuste. No entanto, tanto o R-quadrado quanto o R-quadrado ajustado devem ser interpretados com cautela, pois um valor alto não garante um bom modelo. O modelo ainda pode ser suscetível a problemas como multicolinearidade, viés de variável omitida ou outras violações das premissas de regressão.
Premissas e Limitações
A análise de regressão depende de vários pressupostos chave comuns a diferentes tipos de regressão, incluindo regressão linear, logística, polinomial e extensões de regressão múltipla. Se esses pressupostos não forem atendidos, a precisão e a validade das previsões e conclusões do modelo podem ser limitadas. Portanto, é crucial entender e avaliar esses pressupostos ao realizar uma análise de regressão.
Forma Funcional Apropriada: A relação entre as variáveis dependentes e independentes deve seguir a forma funcional do modelo de regressão. Isso significa uma relação linear para a regressão linear, enquanto uma relação polinomial é assumida para a regressão polinomial. Verificar gráficos de dispersão ou de resíduos pode ajudar a identificar violações deste pressuposto.
Independência das Observações: As observações em um conjunto de dados devem ser independentes entre si. Na autocorrelação (quando observações consecutivas estão relacionadas), o modelo de regressão pode subestimar a verdadeira variabilidade dos dados, levando a estimativas de coeficientes e testes de hipóteses não confiáveis.
Independência dos Erros: Os resíduos (erros) devem ser independentes, o que significa que o erro de uma observação não deve influenciar o erro de outra. Se os erros estiverem correlacionados, os erros padrão dos coeficientes podem ser subestimados, levando a inferências incorretas e intervalos de confiança.
Homocedasticidade (para regressão linear e polinomial): A variância dos resíduos deve ser constante em todos os níveis das variáveis independentes. Se a variância mudar (um fenômeno chamado heterocedasticidade), os erros padrão dos coeficientes podem ser tendenciosos, afetando os testes de hipótese e os intervalos de confiança.
Normalidade dos Resíduos (para regressão linear e polinomial): Os resíduos (ou seja, as diferenças entre os valores observados e previstos) devem seguir uma distribuição normal. Violações da normalidade podem afetar os testes de hipótese e a validade dos intervalos de confiança.
Ausência de Multicolinearidade (para as regressões múltiplas): As variáveis independentes não devem ser altamente correlacionadas entre si. A multicolinearidade pode causar estimativas de coeficientes instáveis e dificultar a interpretação das contribuições individuais de cada variável.
Função de Ligação Corretamente Especificada (para regressão logística): A função de ligação deve ser corretamente definida na regressão logística para transformar os valores previstos em probabilidades. O uso de uma função de ligação incorreta pode levar a estimativas de coeficientes tendenciosas e previsões imprecisas.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Interpretando os Resultados da Análise de Regressão
Compreender e interpretar os resultados de uma análise de regressão é crucial para tomar decisões melhores e tirar conclusões significativas. Aqui estão alguns aspectos chave a considerar ao interpretar os resultados de qualquer modelo de regressão, incluindo regressão linear, logística, polinomial e múltipla:
Estimativas dos Coeficientes: Os coeficientes representam o efeito de cada variável independente sobre a variável dependente, mantendo todas as outras variáveis constantes. Em regressões lineares e polinomiais, os coeficientes indicam a mudança na variável dependente para um aumento unitário na variável independente. Na regressão logística, os coeficientes representam a mudança nas log-odds do resultado para um aumento unitário na variável independente.
Significância dos Coeficientes: Testes de hipótese, como testes t ou z, são realizados para determinar a significância estatística dos coeficientes. Um coeficiente estatisticamente significativo sugere que a variável independente tem um impacto significativo sobre a variável dependente. Um coeficiente não significativo implica que a variável independente pode não contribuir significativamente para o modelo.
Intervalos de Confiança: Os intervalos de confiança estimam a faixa dentro da qual o coeficiente populacional provavelmente se encontrará. Intervalos mais estreitos sugerem estimativas mais precisas, enquanto intervalos mais amplos indicam maior incerteza.
Estatísticas de Ajuste do Modelo: Métricas de ajuste do modelo, como R-quadrado, R-quadrado ajustado ou o Critério de Informação de Akaike (AIC), podem ajudar a avaliar o desempenho geral do modelo. Essas métricas devem ser consideradas juntamente com outras medidas diagnósticas e gráficos para avaliar a adequação do modelo.
Análise de Resíduos: Examinar os resíduos pode revelar padrões ou tendências que sugerem violações das premissas de regressão ou áreas onde o modelo não se ajusta bem aos dados. Gráficos de resíduos, gráficos de probabilidade normal e gráficos de autocorrelação podem ser usados para diagnosticar problemas potenciais e orientar a melhoria do modelo.
Outliers: Os outliers podem impactar significativamente o modelo de regressão. Identificar e tratar essas observações, excluindo-as quando representarem erros de medida ou registro ou utilizando técnicas de regressão robustas, pode ajudar a melhorar o desempenho do modelo.
Validação e Generalização: Técnicas de validação podem ser usadas para avaliar o desempenho do modelo com novos dados, ajudando a medir sua generalização e prevenir o sobreajuste.
Aplicações Práticas da Análise de Regressão
A análise de regressão é uma ferramenta estatística poderosa com muitas aplicações práticas em diversas áreas. A análise de regressão pode ajudar a informar tomadas de decisão, otimizar processos e prever resultados futuros modelando a relação entre as variáveis dependentes e independentes. Aqui estão alguns exemplos de como a análise de regressão é usada em várias indústrias:
Finanças e Economia: Em finanças, a análise de regressão pode ser usada para modelar a relação entre os preços das ações e indicadores econômicos, como taxas de juros ou taxas de desemprego. Isso pode ajudar os investidores a tomar melhores decisões sobre alocação de portfólio e gerenciamento de riscos. Além disso, os economistas podem usar a regressão para estudar o impacto das políticas monetárias e fiscais no crescimento econômico e na inflação.
Marketing e Vendas: Modelos de regressão podem ser empregados para analisar a eficácia de campanhas de marketing, entender o comportamento do consumidor e prever vendas. Por exemplo, as empresas podem usar a regressão para determinar o impacto dos gastos com publicidade nas vendas, permitindo-lhes otimizar seu orçamento de marketing para obter o máximo retorno sobre o investimento.
Saúde: A análise de regressão explora a relação entre as características dos pacientes e os resultados de saúde. Isso pode ajudar a identificar fatores de risco de doenças, melhorar decisões de tratamento e otimizar o cuidado com o paciente. Por exemplo, a regressão logística pode prever a probabilidade de um paciente desenvolver uma condição específica com base em variáveis demográficas e clínicas.
Manufatura e Controle de Qualidade: A análise de regressão pode otimizar processos de fabricação, melhorar a qualidade do produto e reduzir os custos de produção. Ao modelar a relação entre variáveis de processo e características do produto, as empresas podem identificar as condições ótimas para alcançar as especificações desejadas do produto enquanto minimizam o desperdício e o consumo de recursos.
Recursos Humanos: Em gestão de RH, a análise de regressão pode ser usada para entender os fatores que influenciam o desempenho, a retenção e a satisfação dos funcionários. Isso pode ajudar as organizações a desenvolver estratégias de recrutamento, treinamento e engajamento de funcionários direcionadas, melhorando, em última análise, a produtividade e reduzindo a rotatividade.
Análise Esportiva: Modelos de regressão estão sendo cada vez mais usados na análise esportiva para avaliar o desempenho dos jogadores, informar decisões de treinamento e otimizar estratégias de equipe. Por exemplo, a análise de regressão múltipla pode quantificar a contribuição das estatísticas de jogadores individuais para o sucesso da equipe, ajudando técnicos e gerentes a tomar decisões mais informadas sobre o elenco.
Ciência Ambiental: Em pesquisas ecológicas, a análise de regressão pode ser empregada para modelar a relação entre fatores ambientais, como temperatura ou precipitação, e resultados ecológicos, como distribuição de espécies ou produtividade do ecossistema. Isso pode informar esforços de conservação, gestão de recursos naturais e desenvolvimento de políticas.
Armadilhas e Equívocos Comuns na Análise de Regressão
Embora a análise de regressão seja uma ferramenta estatística poderosa e amplamente utilizada, ela apresenta desafios e potenciais armadilhas. Estar ciente desses equívocos e problemas comuns pode ajudar os profissionais a evitar erros e melhorar a qualidade de suas análises:
Correlação vs. Causalidade: Um equívoco comum na análise de regressão é acreditar que correlação implica causalidade. Embora a regressão possa identificar relações entre variáveis, isso não necessariamente prova um vínculo causal. Estabelecer causalidade requer uma compreensão mais profunda dos mecanismos subjacentes e frequentemente envolve desenhos experimentais ou análises adicionais.
Sobreajuste: Construir um modelo que é muito complexo ou inclui muitas variáveis independentes pode levar ao sobreajuste, onde o modelo captura ruído nos dados em vez das relações subjacentes. Modelos sobreajustados apresentam desempenho ruim em novos dados e podem levar a conclusões enganosas. Para prevenir o sobreajuste, considere usar validação cruzada, regularização ou seleção de modelo baseada em critérios de informação como AIC ou BIC.
Multicolinearidade: Quando as variáveis independentes estão altamente correlacionadas, torna-se difícil interpretar a contribuição individual de cada variável para o modelo. A multicolinearidade pode levar a estimativas instáveis e erros padrão inflados. Detectar multicolinearidade através de fatores de inflação de variância (VIFs) ou matrizes de correlação, e abordá-la por meio de técnicas como seleção de variáveis ou redução de dimensionalidade, pode ajudar a melhorar a interpretação e o desempenho do modelo.
Viés de Variável Omitida: Excluir variáveis importantes do modelo de regressão pode resultar em estimativas de coeficientes tendenciosas e conclusões enganosas. Para evitar o viés de variável omitida, certifique-se de incluir todas as variáveis relevantes na análise. Considere usar regressão passo a passo ou técnicas de seleção de modelo para identificar os preditores mais importantes.
Violação de Premissas: Ignorar ou falhar em testar as premissas da análise de regressão pode levar a resultados não confiáveis. É essencial avaliar a validade das suposições, como linearidade, independência de erros, normalidade e homocedasticidade, e empregar técnicas alternativas ou transformações se necessário.
Extrapolação: Usar modelos de regressão para fazer previsões além do alcance dos dados observados pode ser arriscado, pois as relações entre variáveis podem não se manter em regiões não observadas. Tenha cautela ao extrapolar previsões e considere as limitações do modelo e o potencial para fatores imprevistos influenciarem o resultado.
Interpretação Incorreta dos Coeficientes: Interpretar coeficientes de regressão sem considerar a escala das variáveis ou a função de ligação (no caso de regressão logística) pode levar a confusão e conclusões incorretas. Certifique-se de que a interpretação dos coeficientes seja apropriada ao contexto e considere as unidades de medida, a direção do efeito e a magnitude da relação.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Conclusão
A análise de regressão é uma ferramenta estatística poderosa e versátil que permite aos profissionais modelar as relações entre variáveis, fazer previsões e informar a tomada de decisões em diversas áreas. Compreendendo os conceitos fundamentais, como de variáveis dependente e independente, coeficientes e adequação do modelo, os analistas podem selecionar o tipo apropriado de modelo de regressão para seus dados, incluindo regressão linear, logística, polinomial e múltipla.
No entanto, é crucial estar ciente das premissas e limitações da análise de regressão e interpretar os resultados cuidadosamente para evitar armadilhas e equívocos comuns. Considerando as suposições, abordando questões como multicolinearidade e sobreajuste, e utilizando técnicas como validação cruzada e regularização, os praticantes podem construir modelos mais precisos e generalizáveis que contribuem com insights valiosos e promovem a tomada de decisões baseada em dados.
Artigos Recomendados
Pronto para expandir seu conhecimento? Confira nosso blog para mais artigos relevantes e aprofunde seu entendimento desses testes estatísticos cruciais. Aproveite a oportunidade para aprimorar suas habilidades de análise de dados e promover uma tomada de decisão mais informada. Leia agora!
- Premissas da Regressão Linear: Um Guia
- Guia Abrangente sobre Testes de Hipóteses
- Tamanho Amostral: Regressão Logística Binária
- Quais São as Premissas da Regressão Logística?
- Regression Analysis – an overview (Link Externo)
- O que é uma Variável Independente em um Experimento?
- Desvendando a Variável Dependente na Pesquisa Científica
FAQ: O que é Análise de Regressão
A análise de regressão é uma abordagem estatística para modelar relações entre as variáveis dependente e independentes para previsão e tomada de decisão.
Os principais tipos são regressão linear, logística e polinomial — podendo estas serem simples ou múltiplas — cada um adequado a diferentes tipos de dados e objetivos.
Correlação mede a força e direção de uma relação entre variáveis, enquanto causalidade implica que uma variável influencia diretamente a outra.
As premissas incluem linearidade, normalidade, independência de erros e homocedasticidade, que devem ser validadas para resultados confiáveis.
Quando variáveis independentes são altamente correlacionadas, ocorre multicolinearidade, tornando difícil interpretar as contribuições individuais. Pode ser abordada usando seleção de variáveis ou técnicas de redução de dimensionalidade.
Sobreajuste ocorre quando um modelo captura ruído em vez de relações subjacentes, resultando em baixa generalização. Pode ser prevenido usando validação cruzada, regularização ou seleção de modelo.
Coeficientes representam o efeito de variáveis independentes sobre a variável dependente, mantendo outras variáveis constantes. A interpretação depende do tipo de regressão e das escalas das variáveis.
A análise dos resíduos examina os erros (ou resíduos, diferenças entre valores observados e previstos) para identificar padrões, tendências ou violações das premissas de regressão, orientando a melhoria do modelo.
A análise de regressão é amplamente utilizada em finanças, marketing, saúde, manufatura, RH, análise esportiva e ciência ambiental.
Armadilhas comuns incluem confundir correlação com causalidade, sobreajuste, multicolinearidade, viés de variável omitida, extrapolação e interpretação incorreta de coeficientes.








