Coeficiente de Determinação x Coeficiente de Correlação na Análise de Dados
O coeficiente de correlação (r) avalia a direção e a força de uma relação linear entre duas variáveis, variando de -1 a 1. Por sua vez, o coeficiente de determinação (R²), com valores que variam de 0 a 1, indica a proporção da variância na variável dependente que é explicada pela variável independente.
Introdução
Neste artigo, exploramos detalhadamente os coeficientes de correlação (r) e de determinação (R²), duas métricas fundamentais em estatística e análise de dados. Ao entender a distinção entre esses coeficientes e como eles são calculados e interpretados, podemos ter insights mais precisos sobre a natureza das relações entre variáveis contínuas.
Destaques do Artigo
- O coeficiente de correlação (r) varia de -1, indicando uma correlação negativa perfeita, a 1, indicando uma correlação positiva perfeita.
- O valor de r quantifica tanto a direção quanto a força da relação linear entre as variáveis.
- O R², que é o quadrado de r, quantifica a proporção de variância na variável dependente que é explicada pela variável independente.
- Os valores do coeficiente de determinação (R²) variam de 0, quando não há variância explicada, a 1, quando toda a variância é explicada.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Cálculo e Interpretação do Coeficiente de Correlação (r)
O coeficiente de correlação (r) é uma medida que quantifica a força e a direção de uma relação linear entre duas variáveis contínuas, variando de -1 a 1. O valor de r revela:
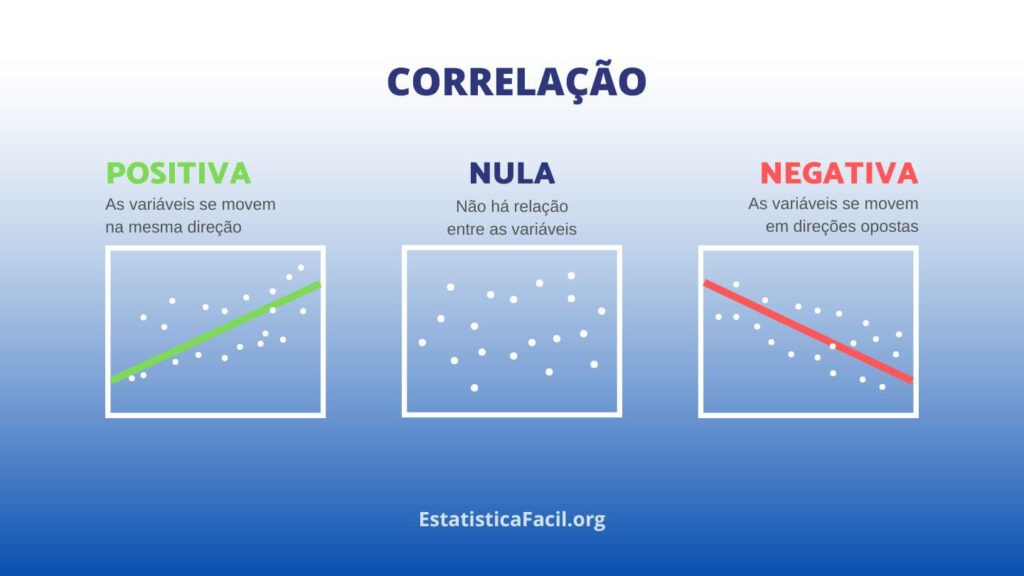
- -1: Indica uma relação linear negativa perfeita.
- 0: Sinaliza a ausência de relação linear.
- 1: Representa uma relação linear positiva perfeita.

Para calcular o coeficiente de correlação, aplica-se a fórmula:
r = Σ[(xi – x̄)(yi – ȳ)] / √[Σ(xi – x̄)² * Σ(yi – ȳ)²]
Nessa fórmula, 𝑥𝑖 e 𝑦𝑖 representam os dados individuais, enquanto x̄ e ȳ são as médias das variáveis X e Y, respectivamente.
Na interpretação do coeficiente de correlação, considera-se:
- Valores positivos indicam uma relação direta entre as variáveis.
- Valores negativos refletem uma relação inversa.
- Valores próximos de 0 demonstram uma relação linear fraca ou ausente.
Cálculo e Interpretação do Coeficiente de Determinação (R²)
O coeficiente de determinação, conhecido como R², é o quadrado do coeficiente de correlação e expressa a proporção da variância na variável dependente que é explicada pela variável independente. O R² varia de 0 a 1, onde:
- 0 indica que o modelo não explica nenhuma variância da variável dependente.
- 1 sugere que o modelo explica completamente a variância da variável dependente.
A fórmula para calcular o coeficiente de determinação é simplesmente:
𝑅²=𝑟²
Ao interpretar R², considere:
- Valores próximos de 1 indicam um alto poder explicativo do modelo.
- Valores próximos de 0 indicam um poder explicativo baixo do modelo.
Coeficiente de Determinação x Coeficiente de Correlação
Assim, na estatística e análise de dados, os coeficientes de correlação (r) e de determinação (R²) são métricas interligadas e cruciais para avaliar as relações entre variáveis. Embora ambos quantifiquem relações, eles se diferenciam quanto ao aspecto que cada um explica sobre a relação entre as variáveis.
Em resumo, o coeficiente de correlação (r) mede a direção e a força de uma relação linear entre duas variáveis, com valores que vão de -1 (correlação negativa perfeita) até 1 (correlação positiva perfeita). Em contrapartida, o coeficiente de determinação (R²) expressa a proporção da variância na variável dependente que é explicada pela variável independente, oscilando entre 0 (nenhuma variância explicada) e 1 (variância completamente explicada). Esse coeficiente, R², corresponde ao quadrado do coeficiente de correlação (R² = r²).

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Conclusão
Ao explorar as nuances e aplicações dos coeficientes de correlação (r) e de determinação (R²), torna-se evidente o papel vital que essas métricas desempenham na análise de dados. Compreender esses coeficientes não apenas enriquece nosso conhecimento estatístico, mas também aprimora nossa capacidade de interpretar e modelar relações entre variáveis. Encorajamos você a aplicar esse conhecimento na prática e a explorar mais conteúdos em nosso blog, para continuar a evoluir na jornada de tomada de decisões baseadas em evidências sólidas e análises rigorosas.
Leitura Recomendada
Deseja aprofundar seus conhecimentos sobre análise de dados? Explore outros artigos relacionados em nosso blog!
- O Desvio Padrão Pode Ser Negativo?
- Premissas da Regressão Linear: Um Guia
- Tamanho Amostral: Regressão Logística Binária
- O Coeficiente de Correlação Pode Ser Negativo?
- Correlação vs. Causalidade: Entendendo a Diferença
- O que é Análise de Regressão? Um Guia Completo para Iniciantes
- Coefficient of Determination vs Coefficient of Correlation (Link Externo)
Perguntas Frequentes (FAQ)
O coeficiente de correlação (r) avalia tanto a direção quanto a intensidade de uma relação linear entre duas variáveis contínuas, podendo variar entre -1 e 1.
O coeficiente de determinação (R²) quantifica a fração da variância na variável dependente que é explicada pela variável independente, com valores entre 0 e 1.
A fórmula para calcular o coeficiente de correlação é: r = Σ[(xi – x̄)(yi – ȳ)] / √[Σ(xi – x̄)² * Σ(yi – ȳ)²]
O coeficiente de determinação, R², é calculado elevando-se o coeficiente de correlação ao quadrado: R² = r².
Não, correlação por si só não implica causalidade, devido à possível presença de fatores de confusão e o acaso.
Não, um coeficiente de correlação baixo pode sugerir a existência de uma relação não linear, em vez de nenhuma relação.
Valores positivos de r indicam uma relação direta entre as variáveis, enquanto valores negativos apontam para uma relação inversa.
Valores de R² próximos de 1 denotam um alto poder explicativo do modelo; valores próximos de 0 indicam um poder explicativo menor.
Não, R² e r têm propósitos distintos e não devem ser utilizados de maneira intercambiável.
Esses coeficientes são utilizados para avaliar a relação entre variáveis, determinar a eficácia de modelos estatísticos e guiar a tomada de decisões baseada em análise de dados.








