Você vai aprender como aplicar corretamente a Regra Empírica (68-95-99,7) na análise de dados e entender os equívocos comuns que deve evitar.
O desvio padrão é uma medida estatística fundamental que auxilia no entendimento da dispersão de dados ao redor da média.
No entanto, existem alguns mal-entendidos frequentes a respeito da Regra Empírica do desvio padrão, os quais podem resultar em análises de dados imprecisas.
Neste guia, desvendaremos a Regra Empírica do desvio padrão e apresentaremos o modo correto de sua aplicação.
Pontos-chave
- O desvio padrão avalia a dispersão de um conjunto de dados.
- 68% dos dados estão dentro de um desvio padrão da média.
- 95% dos dados estão dentro de dois desvios padrão da média.
- 99,7% dos dados estão até três desvios padrão da média.
- A Regra Empírica só é válida para distribuições normais.
Desvio Padrão
O desvio padrão é uma métrica amplamente utilizada para avaliar a dispersão ou variabilidade de um conjunto de dados.
Ele fornece uma ideia de quão distante os dados individuais estão em relação à média do conjunto de dados.
Um desvio padrão pequeno indica que os dados estão fortemente agrupados em torno da média, enquanto um desvio padrão grande sinaliza que os dados estão mais dispersos.
Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Regra Empírica do Desvio Padrão
A Regra Empírica, também conhecida como Regra 68-95-99.7, oferece uma diretriz aproximada para entender a distribuição de dados em uma distribuição normal (gaussiana).
Esta regras se baseia nas características da distribuição normal, que possui simetria e forma de sino.
As regras estabelecem que:
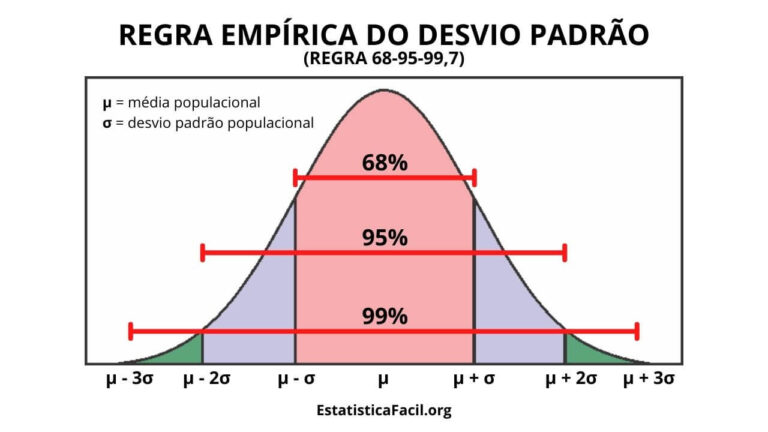
1. Aproximadamente de 68% dos dados estão contidos dentro de um desvio padrão a partir da média (μ ± 1σ).
2. Aproximadamente 95% dos dados estão dentro de dois desvios padrão a partir da média (μ ± 2σ).
3. Aproximadamente 99,7% dos dados se encontram dentro de três desvios padrão da média (μ ± 3σ).
O desvio padrão (σ) é uma medida da variabilidade de um conjunto de dados, e a média (μ) a medida de centralidade do conjunto de dados.
A regra empírica do desvio padrão proporciona um entendimento rápido da distribuição dos dados em uma distribuição normal, facilitando a identificação de outliers.
Equívocos Sobre a Regra Empírica
Existem vários equívocos comuns sobre a Regra Empírica, que podem conduzir à confusão ou interpretação inadequada dos dados. Dentre eles, destacamos:
Aplicabilidade a todas as distribuições
A Regra Empírica é aplicável apenas a distribuições normais (gaussianas). Para outros tipos de distribuições, como as assimétricas ou bimodais, as porcentagens correspondentes a cada desvio padrão a partir da média podem ser diferentes. Assim, é crucial verificar se um conjunto de dados segue uma distribuição normal antes de aplicar a Regra Empírica.
Percentuais exatos
Embora a Regra Empírica ofereça uma estimativa útil para a porcentagem de dados que estão dentro de 1, 2, e 3 desvios padrão a partir da média (68%, 95%, e 99,7%, respectivamente), tais percentuais não são exatos. Eles são aproximações arredondadas, e os percentuais reais podem variar ligeiramente.
Confundindo desvio padrão com erro padrão
O desvio padrão (σ) mede a variabilidade dentro de um conjunto de dados, enquanto o erro padrão (SE) mede a variabilidade de uma estatística amostral (como a média) em diversas amostras da mesma população. Embora ambos sejam baseados no conceito de dispersão, eles servem a propósitos diferentes e não devem ser confundidos.
Ignorando o tamanho da amostra
A Regra Empírica pressupõe que os dados sigam uma distribuição normal. Para tamanhos de amostra pequenos, essa premissa pode não ser válida, e a Regra Empírica pode não se aplicar. Conforme o tamanho da amostra aumenta, o teorema do limite central entra em cena, indicando que a distribuição das médias amostrais se aproxima de uma distribuição normal, independentemente da forma da distribuição da população.
Acreditando que outliers são impossíveis
A Regra Empírica sugere que cerca de 99,7% dos dados estão dentro de três desvios padrão da média. Isso pode, por vezes, ser mal interpretado como indicativo de que outliers além de três desvios padrão são impossíveis. Embora seja raro que dados ultrapassem três desvios padrão, isso ainda pode ocorrer, especialmente em conjuntos de dados grandes.
Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Conclusão
Compreender os equívocos frequentes a respeito da Regra Empírica é crucial para uma interpretação e análise corretas dos dados.
É essencial saber que a Regra Empírica se aplica apenas a distribuições normais e que suas porcentagens são aproximadas, não exatas.
Além disso, o desvio padrão e o erro padrão possuem propósitos distintos e não devem ser confundidos.
O tamanho da amostra tem uma significância importante na determinação da aplicabilidade da Regra Empírica, e a suposição de normalidade deve sempre ser levada em consideração.
Por fim, embora raros, outliers além de três desvios padrão são possíveis e não devem ser descartados de imediato.
Ao nos conscientizarmos desses equívocos e empregarmos a Regra Empírica corretamente, podemos evitar interpretações inadequadas e aprimorar a precisão e a confiabilidade de nossas análises de dados.
Perguntas Frequentes
Q1: O que é desvio padrão? É uma métrica que avalia a dispersão ou variabilidade de um conjunto de dados em relação à sua média.
Q2: O que a Regra 68-95-99.7 (Regra Empírica) representa? É uma diretriz sobre a distribuição dos dados em uma distribuição normal: 68% (1σ), 95% (2σ) e 99,7% (3σ).
Q3: Em que tipo de distribuição a Regra Empírica se aplica? Aplica-se exclusivamente às distribuições normais ou gaussianas.
Q4: As porcentagens da Regra Empírica são exatas? Não, são aproximações arredondadas e os percentuais reais podem variar um pouco.
Q5: Qual a diferença entre desvio padrão e erro padrão? Desvio padrão mede a variabilidade de um conjunto de dados, enquanto erro padrão mede a variabilidade de uma estatística amostral.
Q6: A Regra Empírica é válida para amostras pequenas? Para tamanhos de amostra pequenos, a premissa de normalidade pode não ser válida, tornando a regra menos aplicável.
Q7: Outliers além de três desvios padrão são possíveis? Sim, embora raros, outliers além de três desvios padrão podem ocorrer, especialmente em grandes conjuntos de dados.
Q8: O que acontece quando os dados estão fortemente agrupados em torno da média? Indica um desvio padrão pequeno, mostrando baixa dispersão.
Q9: É seguro aplicar a Regra Empírica em distribuições não normais? Não, em distribuições não normais, as porcentagens podem ser diferentes e levar a interpretações incorretas.
Q10: O que é o teorema do limite central? Indica que a distribuição das médias amostrais se aproxima de uma distribuição normal conforme o tamanho da amostra aumenta.
Baixe GRATUITAMENTE amostras do nosso livro digital!
Aprenda a analisar seus dados com uma metodologia incrível.
O retorno que temos recebido de nossos alunos tem sido excelente!
Clique no link abaixo e saiba mais sobre ele:
ENGLISH VERSION
