Premissas da Regressão Linear: Um Guia
Você aprenderá os fundamentos das premissas da regressão linear e como validá-las usando exemplos práticos do para uma análise de dados eficaz.
A regressão linear é uma técnica para modelar e prever a relação entre uma variável-alvo e uma ou mais variáveis de entrada — ela nos auxilia a compreender como uma alteração nas variáveis de entrada influencia a variável-alvo. A regressão linear pressupõe que essa relação pode ser representada por uma linha reta.
Por exemplo, imagine que você deseja estimar o valor de um imóvel levando em consideração seu tamanho (medido em metros quadrados) e sua idade (em anos). Neste cenário, o preço do imóvel é a variável-alvo (y), enquanto o tamanho e a idade são as variáveis de entrada (X). Utilizando a regressão linear, você pode estimar o impacto do tamanho e da idade no valor do imóvel.
Pontos-chave
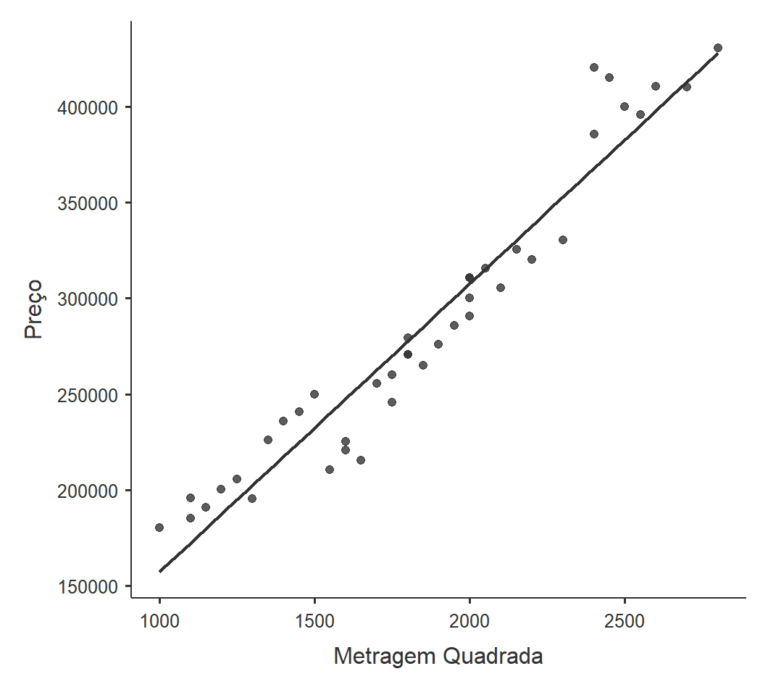
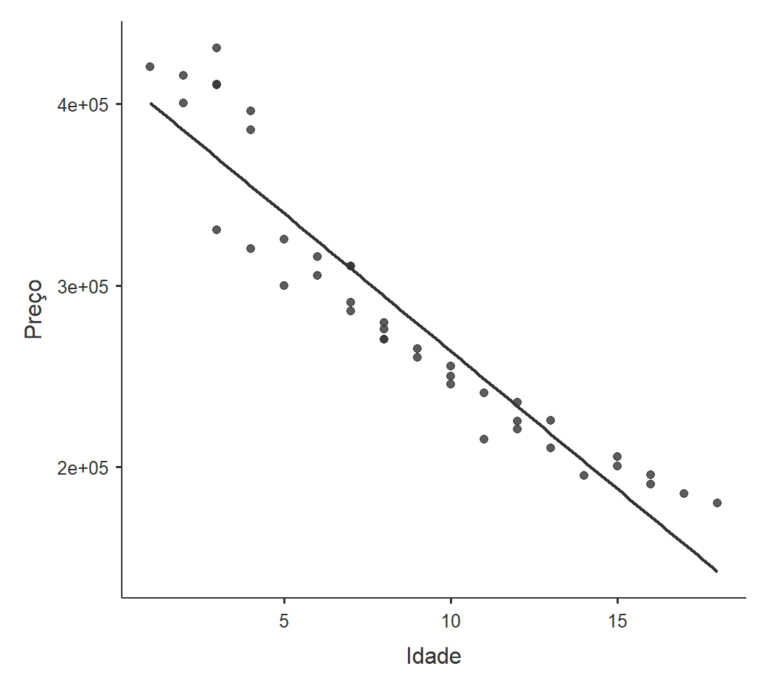
- A linearidade é avaliada através da inspeção visual de scatterplots.
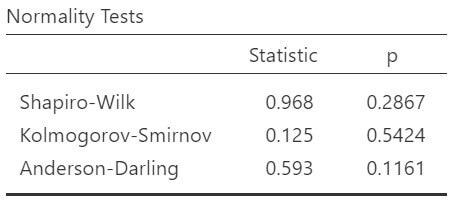
- O teste Shapiro-Wilk verifica a normalidade dos resíduos.
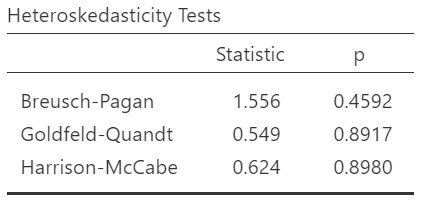
- O teste Breusch-Pagan avalia a homocedasticidade dos erros.
- Estatística Durbin-Watson próxima de 2 sugere erros independentes.
- Baixos valores de VIF e altos de Tolerância indicam mínima multicolinearidade.
Premissas da Regressão Linear
Para que o modelo de regressão linear seja confiável e válido, cinco principais premissas devem ser satisfeitas:
Linearidade
Esta premissa indica que existe uma relação linear entre as variáveis dependente e independente. Em termos mais claros, a mudança na variável dependente deve ser proporcional à mudança na variável independente. A linearidade pode ser avaliada através de gráficos de dispersão ou examinando os resíduos.
Normalidade dos Erros
Os resíduos devem seguir uma distribuição normal com média zero. Esta premissa é fundamental para a realização adequada de testes de hipóteses e para construir intervalos de confiança. A normalidade dos erros pode ser avaliada por métodos visuais, como um histograma ou um gráfico Q-Q, ou através de testes estatísticos, como o teste de Shapiro-Wilk ou o teste de Kolmogorov-Smirnov.
Homocedasticidade
Esta premissa destaca que a variância dos resíduos deve ser constante em todos os níveis da variável independente. Ou seja, a dispersão dos resíduos deve ser semelhante para todos os valores das variáveis independentes. A heterocedasticidade, que viola essa premissa, pode ser identificada usando gráficos de dispersão dos resíduos ou testes formais como o teste de Breusch-Pagan.
Independência dos Erros
Esta premissa estabelece que as observações do conjunto de dados devem ser independentes entre si. Observações podem depender uma da outra quando lidamos com dados temporais ou espaciais devido à sua proximidade temporal ou espacial. Violar essa premissa pode levar a estimativas tendenciosas e previsões não confiáveis. Modelos específicos, como modelos temporais ou espaciais, podem ser mais adequados nesses casos.
Ausência de Multicolinearidade (Regressão Linear Múltipla)
A multicolinearidade ocorre quando duas ou mais variáveis independentes no modelo de regressão linear estão altamente correlacionadas, dificultando determinar o efeito exato de cada variável sobre a dependente. A multicolinearidade pode resultar em estimativas instáveis, erros padrão inflados e dificuldade na interpretação dos coeficientes. É possível utilizar o fator de inflação da variância (VIF) ou matriz de correlação para detectar multicolinearidade. Se estiver presente, considere excluir uma das variáveis correlacionadas, combinar as variáveis correlacionadas ou usar técnicas como a análise de componentes principais (PCA) ou regressão ridge.
| Premissas | Descrição |
|---|---|
| Linearidade | Relação linear entre variáveis dependentes e independentes, verificada usando gráficos de dispersão |
| Normalidade | Distribuição normal dos resíduos, avaliada usando o teste de Shapiro-Wilk |
| Homocedasticidade | Variância constante nos termos de erro, avaliada usando o teste de Breusch-Pagan |
| Independência dos Erros | Termos de erro independentes, verificados usando o teste de Durbin-Watson |
| Independência das Observações | Dados coletados independentemente sem autocorrelação |
| Ausência de Multicolinearidade | Sem multicolinearidade entre variáveis independentes, determinada usando VIF e medidas de Tolerância |

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Exemplo Prático
Aqui está uma demonstração de um problema de modelo de regressão linear com duas variáveis independentes e uma variável dependente. Neste exemplo, modelaremos a relação entre a metragem quadrada de uma casa e sua idade com o seu preço de venda. O conjunto de dados contém a metragem quadrada (X1), a idade (X2) e o preço de venda (y) de 40 casas.
Usaremos a regressão linear múltipla para estimar os efeitos da metragem quadrada e da idade sobre o preço de venda. Abaixo está uma tabela com os dados que você pode copiar e colar em seu programa de análises:
| Casa | Metragem Quadrada | Idade | Preço |
|---|---|---|---|
| 1 | 1500 | 10 | 250000,50 |
| 2 | 2000 | 5 | 300000,75 |
| 3 | 1200 | 15 | 200500,25 |
| 4 | 2500 | 2 | 400100,80 |
| 5 | 1800 | 8 | 270500,55 |
| 6 | 1600 | 12 | 220800,60 |
| 7 | 2200 | 4 | 320200,10 |
| 8 | 2400 | 1 | 420300,90 |
| 9 | 1000 | 18 | 180100,15 |
| 10 | 2000 | 7 | 290700,40 |
| 11 | 1450 | 11 | 240900,65 |
| 12 | 2050 | 6 | 315600,20 |
| 13 | 1150 | 16 | 190800,75 |
| 14 | 2600 | 3 | 410500,50 |
| 15 | 1750 | 9 | 260200,55 |
| 16 | 1550 | 13 | 210700,85 |
| 17 | 2300 | 3 | 330400,45 |
| 18 | 2450 | 2 | 415200,90 |
| 19 | 1100 | 17 | 185300,65 |
| 20 | 1900 | 8 | 275900,80 |
| 21 | 1400 | 12 | 235800,55 |
| 22 | 2100 | 6 | 305300,40 |
| 23 | 1300 | 14 | 195400,25 |
| 24 | 2700 | 3 | 410200,75 |
| 25 | 1700 | 10 | 255600,20 |
| 26 | 1650 | 11 | 215400,60 |
| 27 | 2150 | 5 | 325500,50 |
| 28 | 1250 | 15 | 205700,85 |
| 29 | 2550 | 4 | 395900,90 |
| 30 | 1850 | 9 | 265100,65 |
| 31 | 1350 | 13 | 225900,40 |
| 32 | 1950 | 7 | 285800,15 |
| 33 | 1100 | 16 | 195900,80 |
| 34 | 2800 | 3 | 430700,55 |
| 35 | 1750 | 10 | 245500,20 |
| 36 | 1600 | 12 | 225300,10 |
| 37 | 2000 | 7 | 310700,50 |
| 37 | 2000 | 7 | 310700,50 |
| 38 | 2400 | 4 | 385400,25 |
| 39 | 1800 | 8 | 270500,90 |
| 40 | 1800 | 8 | 279500,25 |
Linearidade
Avalie a premissa de linearidade inspecionando visualmente o gráfico de dispersão da variável dependente (y) contra cada variável independente (X), procurando um padrão linear discernível.
Normalidade dos erros
Avalie a premissa de normalidade conduzindo o teste de Shapiro-Wilk, que avalia a distribuição dos resíduos em busca de desvios significativos de uma distribuição normal.
No teste de Shapiro-Wilk, um valor-p alto (tipicamente acima de 0,05) indica que a distribuição dos resíduos não difere significativamente de uma distribuição normal.
Homocedasticidade
Avalie a suposição de homocedasticidade realizando o teste de Breusch-Pagan, que verifica a presença de variância não constante nos termos de erro.
Um valor-p alto (tipicamente acima de 0,05) sugere que os dados exibem homocedasticidade, com variância constante em diferentes valores.
Independência dos erros
Uma estatística de Durbin-Watson próxima de 2 sugere que os erros são independentes, com autocorrelação mínima presente.
Valores abaixo ou acima de 2 indicam autocorrelação positiva ou negativa, respectivamente.
O valor-p significa que a estatística DW não é significativamente diferente de 2.
*Para evitar violar a suposição de independência das observações, garanta que seus pontos de dados sejam coletados de forma independente e não exibam autocorrelação, que pode ser avaliada usando o teste de Durbin-Watson.
Ausência de multicolinearidade
Avalie a ausência de multicolinearidade usando o Fator de Inflação da Variância (VIF) e medidas de Tolerância. Valores baixos de VIF (tipicamente abaixo de 10) e valores altos de Tolerância (acima de 0,1) indicam que a multicolinearidade não é uma preocupação significativa no modelo de regressão.
Nossos dados indicam a presença de multicolinearidade entre as variáveis idade e metragem quadrada. Precisaremos remover uma delas. A variável a ser removida pode ser determinada de várias maneiras, como testar com regressões lineares simples para ver qual se ajusta melhor ao modelo ou decidir com base na teoria subjacente.
Conclusão
É crucial examinar e tratar essas premissas ao construir um modelo de regressão linear para garantir validade, confiabilidade e interpretabilidade.
Ao compreender e verificar as premissas — linearidade, independência dos erros, homocedasticidade, normalidade dos erros, independência das observações e ausência de multicolinearidade — você pode construir modelos mais precisos e confiáveis, levando a uma melhor tomada de decisão e aprimorando a compreensão das relações entre as variáveis em seus dados.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Perguntas Frequentes
Q1: O que é linearidade em regressão linear? É a premissa de que existe uma relação linear entre a variável dependente e as variáveis independentes.
Q2: Como a normalidade dos erros é avaliada? A normalidade é verificada usando o teste Shapiro-Wilk, que avalia a distribuição dos resíduos.
Q3: O que significa um p-valor alto no teste Shapiro-Wilk? Indica que a distribuição dos resíduos não difere significativamente de uma distribuição normal.
Q4: Como a homocedasticidade é verificada? Através do teste Breusch-Pagan, que verifica a constância da variação dos termos de erro.
Q5: O que a estatística Durbin-Watson indica? Próxima de 2, sugere que os erros são independentes, sem autocorrelação significativa.
Q6: O que são VIF e Tolerância em regressão? VIF (Fator de Inflação da Variância) e Tolerância são métricas para avaliar a multicolinearidade.
Q7: Por que a multicolinearidade é um problema? Pode distorcer ou exagerar os resultados da regressão e tornar os coeficientes instáveis.
Q8: Como é determinada a independência das observações? Usando o teste Durbin-Watson e garantindo que os dados sejam coletados de forma independente.
Q9: Por que é importante verificar as suposições da regressão linear? Garante a validade, confiabilidade e interpretabilidade dos modelos de regressão.
Q10: O que fazer quando a multicolinearidade é detectada entre variáveis? Uma das variáveis pode ser removida ou combinada, ou técnicas como regressão ridge podem ser aplicadas.
Baixe GRATUITAMENTE amostras do nosso livro digital!
Aprenda a analisar seus dados com uma metodologia incrível.
O retorno que temos recebido de nossos alunos tem sido excelente!
Clique no link abaixo e saiba mais sobre ele: