Como Calcular a Média de Forma Simples!
A média é uma medida de tendência central em estatística, representando o centro de um conjunto de dados. Para calcular a média, some todos os valores das observações e divida pelo número total de observações, fornecendo um único valor que reflete a tendência central dos dados.
Introdução
Ao dominar a definição e o cálculo de medidas de tendência central, como a média, mediana e moda, os profissionais podem extrair insights significativos e tomar decisões baseadas em evidências. Através de uma abordagem detalhada, este artigo visa aprofundar o entendimento desses conceitos, fornecendo um guia prático e teórico que é fundamental tanto para novatos quanto para especialistas no campo da análise de dados.
Destaques do Artigo
- A média é uma medida de tendência central que representa o centro de um conjunto de dados.
- Os principais tipos de média são aritmética, geométrica, harmônica e ponderada.
- A média aritmética é calculada somando os dados e dividindo pela sua quantidade.
- A média é sensível a valores discrepantes, que podem distorcer seu valor.
- Média e desvio padrão fornecem insights sobre tendência central e dispersão.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
O que são Medidas de Tendência Central?
Medidas de tendência central são ferramentas estatísticas essenciais que resumem o valor central ou mais representativo de um conjunto de dados. Essas medidas facilitam a compreensão de conjuntos de dados complexos ao destacar um valor que sintetiza a tendência central do conjunto. As principais medidas de tendência central são a média, a mediana e a moda. Cada uma destas medidas proporciona uma visão distinta sobre a distribuição dos dados, sendo fundamental compreender suas diferenças e suas aplicações específicas.
Defina a Média!
A média, comumente conhecida como valor médio, representa um dos mais importantes tipos de medida de tendência central utilizada em estatística. Esta medida serve para descrever o centro de um conjunto de dados. A média do tipo aritmética é a mais comumente utilizada e pode ser facilmente calculada somando-se todos os dados e dividindo essa soma pelo número total de dados. Entender a definição e como calcular a média é crucial para a análise e interpretação de dados. Essa medida pode oferecer informações valiosas sobre as tendências e padrões gerais dentro de um conjunto de dados.
Diferentes Tipos de Média
Embora a média aritmética seja a mais conhecida, existem outros tipos de média que podem ser mais adequados dependendo do contexto. Os principais tipos de média são:
Média Aritmética: Esta é a forma mais comum de média, obtida pela soma de todos os valores numéricos do conjunto de dados e dividindo-se pelo número de observações.
Média Ponderada: Difere da média aritmética pelo fato de cada valor no conjunto de dados ter um peso associado, refletindo sua importância ou relevância no cálculo final. É ideal para situações onde alguns dados são mais significativos que outros, como em médias ponderadas de notas escolares ou em avaliações financeiras.
Média Geométrica: Calculada multiplicando-se todos os valores numéricos e, em seguida, extraindo-se a raiz n-ésima do produto (onde n é o número total de valores). É particularmente útil para analisar dados que variam exponencialmente, como taxas de crescimento.
Média Harmônica: Obtida pelo inverso da média dos inversos dos valores numéricos. É frequentemente utilizada em situações que envolvem médias de razões ou taxas, como em cálculos de velocidade média.
Guia Passo a Passo
Como Calcular a Média Aritmética
Para calcular a média aritmética de forma eficaz, siga estes passos:
- Some todos os valores numéricos presentes no conjunto de dados.
- Conte o total de valores numéricos.
- Divida a soma total pelo número de valores.
Por exemplo, se um conjunto de dados inclui os valores 2, 4, 6, 8, 10, a média aritmética é calculada assim:
= (2 + 4 + 6 + 8 + 10) / 5
= 30 / 5
= 6
Portanto, a média deste conjunto de dados é 6 (seis).
Média vs. Mediana vs. Moda
As medidas de tendência central — média, mediana e moda — embora compartilhem o objetivo comum de representar o centro de um conjunto de dados, apresentam características e aplicações distintas:
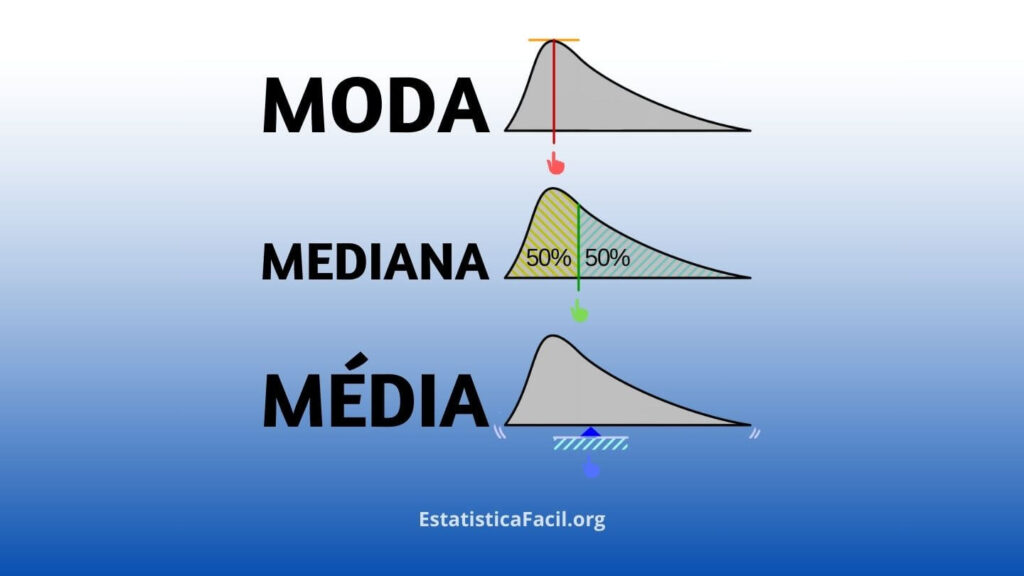
Média: É a soma de todos os valores dividida pelo número de observações no conjunto de dados. A média é particularmente sensível a valores extremos, que podem desviar significativamente seu cálculo.
Mediana: Corresponde ao valor que ocupa a posição central em um conjunto de dados ordenados. Por não ser afetada por valores extremos, é mais indicada para análises de conjuntos de dados assimétricos.
Moda: Representa o valor que ocorre com maior frequência em um conjunto de dados. É especialmente útil para análise de dados categóricos ou para determinar o item mais comum em uma distribuição.
O Papel da Média na Estatística Inferencial
Na estatística inferencial, a média desempenha um papel crucial na estimativa de parâmetros populacionais a partir de dados amostrais. Ela é essencial em processos como testes de hipóteses e cálculo de intervalos de confiança, possibilitando que pesquisadores façam inferências válidas sobre populações maiores com base em amostras. A média é frequentemente utilizada em testes estatísticos, como o teste t e a ANOVA, para comparar médias entre diferentes grupos ou condições.
A Interação Entre Média e Desvio Padrão
A média e o desvio padrão são medidas estatísticas intimamente ligadas que oferecem uma visão completa da tendência central e da dispersão em um conjunto de dados. Enquanto a média indica o ponto central, o desvio padrão mede quão espalhados estão os dados em relação a esse centro. Um desvio padrão pequeno sugere que os dados estão concentrados próximos à média, enquanto um valor alto indica uma dispersão maior. Entender essa relação é fundamental para a interpretação precisa dos dados e para a tomada de decisões informadas.


Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Conclusão
Dominar os conceitos fundamentais, como a definição e cálculo da média, é indispensável para quem trabalha com dados, formando a base para o entendimento de técnicas estatísticas mais complexas. Ao conhecer os diversos tipos de média e seu papel na estatística inferencial, bem como a interação com outras medidas de tendência central e o desvio padrão, estaremos adequadamente preparados para uma análise e interpretação eficazes dos dados. Lembre-se sempre de considerar essas inter-relações para garantir uma análise robusta e abrangente dos conjuntos de dados.
Leitura Recomendada
Aprofunde seus conhecimentos em estatística e análise de dados: visite nosso blog para ler outros artigos informativos sobre temas relacionados.
- O que o Desvio Padrão Significa?
- O Desvio Padrão Pode Ser Negativo?
- Sobre a Regra Empírica do Desvio Padrão
- Desvendando o Desvio Padrão: Um Guia Prático
- Tamanho Amostral Para o Teste t: Como Calcular?
- Estatística vs Parâmetro: Um Guia Completo com Perguntas Frequentes
- Defining the Mean in Simple Terms! Mastering the Basics (Link Externo)
FAQ: Definindo a Média
A média, também conhecida como valor médio, é uma medida de tendência central que indica o ponto central de um conjunto de dados.
Para calcular a média aritmética, some todos os valores das observações e divida pelo número total de observações.
Existem várias formas de calcular a média, incluindo a média aritmética, geométrica, harmônica e ponderada, cada uma adequada a diferentes situações estatísticas.
A média geométrica é mais apropriada para dados que crescem ou diminuem a uma taxa constante, típico de situações como retornos de investimentos ou crescimento populacional.
A média harmônica é ideal em cenários que envolvem médias de taxas ou proporções, como cálculos de velocidade média ou eficiência.
A média ponderada é uma variação da média aritmética que atribui pesos diferentes aos pontos de dados, considerando a importância ou relevância de cada um.
Enquanto a média é o valor médio dos dados, a mediana é o valor central quando os dados são ordenados, e a moda é o valor que aparece com mais frequência.
Sim, a média pode ser significativamente afetada por valores extremos ou atípicos, o que pode distorcer a representação da tendência central.
Na estatística inferencial, a média é usada para estimar parâmetros populacionais, realizar testes de hipóteses e calcular intervalos de confiança, proporcionando uma base para inferências sobre uma população maior.
A média indica a localização central dos dados, enquanto o desvio padrão descreve a variabilidade ou dispersão dos dados em relação a essa média.








