O que é Estatística t, Teste t e Distribuição t?
Você compreenderá os princípios da estatística t e aprenderá como aplicá-los em análises de dados práticas para obter insights relevantes.
A estatística é a espinha dorsal da análise de dados, e a estatística t, oriunda da distribuição t, é um dos seus pilares fundamentais.
Essa ferramenta não apenas desempenha um papel vital em testes de hipóteses, particularmente nos testes t, mas também é a chave para entender como e por que certas conclusões são retiradas de conjuntos de dados.
Dominar a estatística t é mais do que uma mera habilidade acadêmica; é uma necessidade para qualquer um que queira analisar dados com precisão e confiança.
Neste artigo, você não só compreenderá a estatística t de forma aprofundada, mas também estará pronto para enfrentar questões complexas, tomar decisões informadas e realizar análises robustas e precisas.
Pontos-chave
- Testes t avaliam diferenças entre médias amostrais.
- A estatística t considera desvio padrão e tamanho da amostra.
- Testes t requerem a verificação de premissas como normalidade.
- P-valores baixos sugerem diferenças estatisticamente significativas.
- Erros comuns incluem assumir normalidade e ignorar premissas.
Estatística t
A estatística t, também conhecida como valor t ou t de Student, é uma medida que nos ajuda a determinar quão grande é a diferença entre as médias de duas amostras, considerando a variabilidade nos dados.
Em outras palavras, ela compara a diferença observada entre as médias das amostras com o que poderíamos esperar por acaso. Se essa diferença for significativamente grande, concluímos que as médias das populações das quais as amostras foram retiradas provavelmente são diferentes.
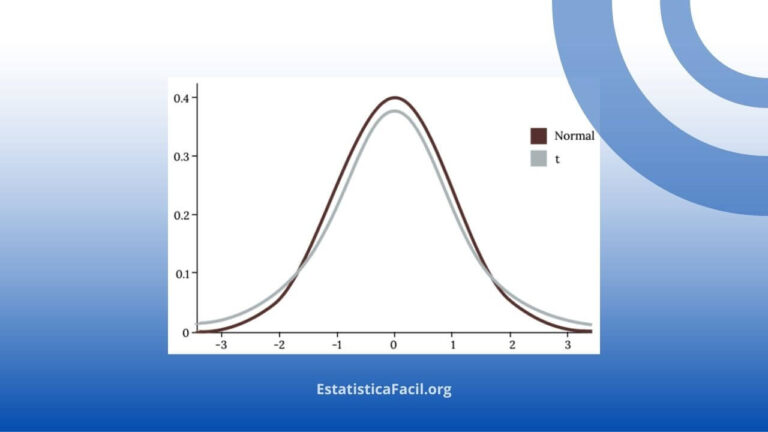
Distribuição t
A distribuição t, também conhecida como distribuição de Student, é uma das distribuições de probabilidade mais importantes no campo da estatística, especialmente quando se trata de inferir sobre uma população a partir de uma amostra pequena.
Origem: A distribuição t foi introduzida por William Sealy Gosset sob o pseudônimo “Student” em 1908. Ele estava trabalhando na empresa de cervejaria Guinness e desenvolveu esta distribuição para lidar com problemas estatísticos envolvendo pequenas amostras.
Teste t
O teste t é um instrumento refinado de análise que se vale da estatística t para confrontar as médias de dois conjuntos de dados. O que ele busca discernir é a natureza da variação entre esses conjuntos: é uma diferença genuinamente significativa? Ou poderia essa variação ser atribuída simplesmente ao capricho do acaso?
Há três tipos de teste t:
Teste t de Uma Amostra: O teste t de uma amostra confronta a média de uma única amostra com uma média populacional já conhecida. Este tipo de teste é frequentemente adotado quando os pesquisadores desejam verificar se a média da amostra diverge de maneira significativa de um valor hipotetizado. Aqui, a estatística t é determinada comparando-se a média da amostra com a média da população, levando em consideração o tamanho da amostra e seu desvio padrão.
Teste t para Amostras Independentes: Este teste, também conhecido como teste t de duas amostras, é aplicado ao se comparar as médias de duas amostras independentes. O principal objetivo é averiguar se existe uma diferença significativa entre as médias das populações das quais as amostras foram extraídas. Para este teste, a estatística t é calculada considerando-se a discrepância entre as médias das amostras, suas variâncias e os respectivos tamanhos das amostras.
Teste t para Amostras Emparelhadas: O teste t para amostras emparelhadas, ou teste t para amostras dependentes, é indicado para comparação das médias de duas amostras relacionadas. Este teste é utilizado quando as observações são feitas em pares, como medições antes e depois de um tratamento, ou sujeitos pareados em designs experimentais. Para este teste, a estatística t é derivada considerando-se as diferenças entre as observações emparelhadas e suas médias, bem como o desvio padrão.
Premissas do Teste t
Garantir que as premissas abaixo sejam atendidas permite aplicar os testes t e a estatística t em suas pesquisas e análises de dados, conduzindo a conclusões válidas e confiáveis.
Dados em Escala de Intervalo ou Razão: Os testes t são projetados para dados contínuos que podem ser medidos em uma escala de razão ou intervalo. Estes tipos de dados possuem intervalos iguais entre os valores e um ponto zero significativo.
Independência das Observações: As observações nas amostras devem ser independentes entre si. Isso implica que a ocorrência de uma observação não deve influenciar a probabilidade de outra observação acontecer. No teste t para amostras independentes, as amostras devem ser selecionadas de forma aleatória e não relacionadas entre si. Para o teste t de amostras emparelhadas, cada par de observações deve ser independente dos outros pares.
Normalidade: Os dados devem ter uma distribuição aproximadamente normal, especialmente para tamanhos de amostras pequenos. Este pressuposto sugere que a distribuição de amostragem das médias segue uma distribuição normal ou quase normal. Embora os testes t sejam considerados robustos a desvios moderados da normalidade, violações graves podem afetar a precisão dos resultados do teste.
Homogeneidade das Variâncias: No teste t para amostras independentes, as variâncias das duas populações comparadas devem ser iguais ou, pelo menos, aproximadamente iguais. Esse pressuposto é conhecido como homogeneidade das variâncias. Se esse pressuposto for violado, testes alternativos, como o teste t de Welch, podem ser empregados, pois este último não exige variâncias iguais.
Graus de Liberdade
Os graus de liberdade representam um conceito fundamental na estatística e têm implicações profundas no cálculo da estatística t e na determinação dos valores críticos em testes t.
Mas, o que são exatamente os graus de liberdade? São o número de valores numa análise que têm a liberdade de variar sem infringir qualquer regra estabelecida — em outras palavras, são as observações independentes que podem ser usadas para estimar um parâmetro.
Exemplo:
Imagine que você tem cinco amigos e está tentando calcular a média das idades deles. Você sabe que a média de suas idades é 25 anos. Se você souber a idade de quatro desses amigos, você poderá facilmente calcular a idade do quinto amigo, mesmo sem ninguém te dizer qual é.
Por exemplo: Amigo 1: 24 anos; Amigo 2: 25 anos; Amigo 3: 26 anos; e Amigo 4: 23 anos.
Usando a informação de que a média é 25 anos, podemos calcular a idade do Amigo 5. Se somarmos as idades dos quatro primeiros amigos, obtemos um total de 98 anos. Para que a média das cinco idades seja 25 anos, o total combinado deve ser 125 anos (25 anos x 5 amigos). Isso significa que o Amigo 5 tem 27 anos (125 – 98 = 27).
Neste exemplo, os graus de liberdade são 4. Isso porque podemos escolher qualquer idade para os primeiros quatro amigos, mas depois que essas idades forem determinadas, a idade do quinto amigo é fixada pela média que conhecemos. Portanto, só temos “liberdade” para variar as idades de 4 dos 5 amigos.
No universo dos testes t, os graus de liberdade determinam a forma específica da distribuição t, essencial para calcular os valores p e tomar decisões estatísticas sobre as diferenças entre grupos.
Como calculamos os graus de liberdade para diferentes testes t:
Teste t de Uma Amostra: Simplesmente subtrai-se um do tamanho total da amostra. Matematicamente falando: gl = n – 1.
Teste t para Amostras Independentes: Neste cenário, temos duas amostras diferentes. A fórmula considera o tamanho de ambas as amostras: gl = n1 + n2 – 2.
Teste t para Amostras Emparelhadas: Aqui, comparamos dois conjuntos de observações do mesmo grupo, como um “antes e depois”. Os graus de liberdade são calculados subtraindo um do número total de pares: gl = n – 1.
A correta compreensão e aplicação dos graus de liberdade não apenas asseguram a precisão da sua análise, mas também a confiabilidade das conclusões extraídas dela.
Estatística t, Valor de p e Intervalos de Confiança
Estes três componentes formam a espinha dorsal da inferência estatística, permitindo aos pesquisadores e analistas de dados não apenas identificar diferenças significativas em seus conjuntos de dados, mas também entender o contexto e a relevância dessas diferenças.
1. Estatística t:
Definição: Originada da distribuição t, a estatística-t quantifica a diferença entre médias amostrais, levando em consideração o desvio padrão e o tamanho da amostra.
Aplicação: Usada principalmente em testes t para contrastar médias amostrais, ela serve como um índice para avaliar o quão longe a nossa amostra está da população sob a hipótese nula.
2. Valor de p:
Definição: Uma métrica que indica a probabilidade de observar um resultado, como o obtido (ou mais extremo), assumindo que a hipótese nula (H0) é verdadeira.
Interpretação: Um p-valor pequeno — frequentemente, menor que 0.05 — sugere que os dados observados são inconsistentes com a hipótese nula (H0), permitindo-nos rejeitá-la em favor da hipótese alternativa (H1). Portanto, um p-valor baixo sinaliza uma diferença estatisticamente significativa.
3. Intervalos de Confiança:
Definição: Uma estimativa de intervalo que indica a faixa dentro da qual esperamos que o verdadeiro valor da população esteja, com uma certa confiança (como 95%).
Interpretação: Em testes t, esses intervalos nos oferecem uma faixa de valores prováveis para as diferenças entre as médias populacionais ou a média da população em si. A amplitude desse intervalo é influenciada por fatores como a estatística-t, o tamanho da amostra e a variabilidade dos dados.
Relação Integrada:
A estatística-t nos fornece uma métrica de diferença que é, então, avaliada em termos de sua probabilidade sob a hipótese nula — daí surge o p-valor.
Ao mesmo tempo, a estatística-t alimenta a construção dos intervalos de confiança, proporcionando uma visão mais ampla da diferença, não apenas em termos de significância, mas também de magnitude e relevância prática.
Em suma, ao combinar a estatística-t, o p-valor e os intervalos de confiança, obtemos uma imagem completa e multidimensional da diferença observada, auxiliando na tomada de decisões informadas e na interpretação precisa dos resultados.
Passos e Exemplos para Teste de Hipóteses com Estatística-t
O teste de hipóteses é uma ferramenta crucial da estatística inferencial, proporcionando decisões fundamentadas em dados amostrais.
Etapas para conduzir o teste de hipóteses usando a estatística-t:
Estabeleça as hipóteses:
- Hipótese nula (H0): Sugere que não existe uma diferença significativa entre as médias populacionais ou que a média da amostra é a mesma do valor proposto.
- Hipótese alternativa (H1): Propõe que pode existir uma diferença significativa entre as médias.
Seleção do teste t correto:
- Escolha o tipo de teste t que se alinha com o design da sua pesquisa, seja ele para uma única amostra, amostras independentes ou amostras pareadas.
Confirmação das premissas:
- Assegure-se de que os dados atendam às premissas necessárias, como independência das observações, normalidade e, quando aplicável, homogeneidade das variâncias.
Computação da estatística-t:
- Utilizando os dados da amostra, calcule a estatística-t conforme a formulação específica do teste t selecionado.
Determinação dos graus de liberdade (df):
- Baseie-se no tamanho da amostra ou amostras para calcular os graus de liberdade.
Obtenção do p-valor:
- Utilize a estatística-t e os graus de liberdade para identificar o p-valor correspondente na distribuição t.
Comparação com o nível de significância (α):
- Se o p-valor for menor que o nível de significância definido (comumente 0,05), rejeite a hipótese nula.
Ilustração Prática: Imagine que deseja avaliar se um novo método de ensino eleva as notas dos alunos.
Coleta-se uma amostra de 25 alunos submetidos ao novo método e compara-se a média das suas notas à média populacional reconhecida de 80.
Para esta situação, utiliza-se o teste t para uma amostra.
- H0: μ = 80; H1: μ ≠ 80.
- Selecionado o teste t para uma única amostra.
- Verificadas e validadas as premissas.
- Resultado da estatística-t é de 2,5.
- Graus de liberdade determinados como: df = 24.
- Com base na estatística-t e df, o p-valor é de 0,019.
- Dado que 0,019 é menor que 0,05, rejeitamos H0.
Conclusão: As evidências apontam para uma melhoria significativa nas notas dos alunos devido ao novo método de ensino.
Comparação entre Testes-t e Testes-z
Ao abordar a análise de dados e a escolha de testes estatísticos, é essencial compreender as diferenças e aplicações dos testes t e z. Aqui, delineamos os pontos chave que diferenciam esses dois testes paramétricos, frequentemente utilizados para comparar médias.
Variação Populacional:
- Testes t: São utilizados quando a variância (ou desvio padrão) da população é desconhecida.
- Testes z: São aplicados quando a variância da população é conhecida.
Tamanho da Amostra:
- Testes t: São mais adequados para amostras menores, geralmente quando n < 30.
- Testes z: São mais apropriados para amostras maiores, onde o Teorema do Limite Central garante que a distribuição das médias amostrais aproxima-se de uma distribuição normal.
Distribuição Associada:
- Testes t: Baseiam-se na distribuição t, que se adapta mais eficientemente à variabilidade de amostras menores com caudas mais largas.
- Testes z: Utilizam a distribuição normal padrão.
Graus de Liberdade:
- Testes t: Requerem o cálculo dos graus de liberdade, que influenciam diretamente a forma da distribuição t. Este aspecto é fundamental para determinar os valores críticos do teste.
- Testes z: Não envolvem graus de liberdade, uma vez que se baseiam na distribuição normal padrão.
Aplicações Reais do Teste t
O entendimento correto do teste t e sua função na estatística é fundamental para perceber o seu impacto prático em diversos campos de atuação.
Vamos detalhar algumas áreas em que o teste t desempenha um papel crucial:
Economia e Finanças: Investidores e economistas utilizam o teste t para analisar a eficácia de estratégias de investimento ou para avaliar o impacto de políticas econômicas sobre indicadores de mercado.
Manufatura: Manter a qualidade do produto é essencial. O teste t pode ser usado para comparar lotes de produtos, garantindo que sua qualidade permaneça consistente ao longo do tempo ou após mudanças no processo de fabricação.
Saúde e Farmacologia: Na pesquisa clínica, o teste t é uma ferramenta valiosa. Seja ao comparar a eficácia de um novo medicamento com um placebo ou ao analisar os resultados de diferentes procedimentos médicos, este teste ajuda os profissionais a tomarem decisões baseadas em dados.
Recursos Humanos: A gestão de talentos se beneficia muito das análises estatísticas. Ao implementar um novo programa de treinamento, o departamento de RH pode usar o teste t para verificar se houve um aumento significativo na performance ou satisfação dos funcionários.
Marketing: Para as empresas, entender o comportamento do consumidor é crucial. Se uma companhia quer saber se uma nova campanha publicitária é mais eficaz do que a anterior, o teste t pode ajudar a determinar se as mudanças nas vendas ou no engajamento dos clientes são realmente significativas.
Educação: O setor educacional frequentemente enfrenta o desafio de avaliar novos métodos de ensino. Usando o teste t, é possível comparar a eficácia de diferentes abordagens pedagógicas. Por exemplo, ao introduzir uma nova técnica de ensino, pode-se usar o teste t para determinar se ela realmente melhora os resultados dos alunos em relação aos métodos tradicionais.
Erros Comuns no Uso do Teste t
A aplicação correta do teste t é crucial para obter resultados confiáveis. No entanto, existem várias armadilhas comuns que os pesquisadores devem evitar. Aqui, detalhamos alguns dos erros mais recorrentes e como evitá-los:
Presumindo Normalidade Sem Verificação:
- Acreditar que os dados são normalmente distribuídos sem fazer a verificação apropriada é um erro frequente. Apesar do Teorema do Limite Central sugerir que a distribuição das médias das amostras se aproxima da normalidade à medida que o tamanho da amostra aumenta, é crucial para amostras pequenas validar essa suposição.
Desconsiderando Premissas do Teste:
- O teste t vem com várias suposições (como independência das observações e homogeneidade das variâncias para amostras independentes). Ignorar ou não avaliar essas suposições pode resultar em análises enganosas.
Seleção Inapropriada do Teste t:
- Utilizar o teste t quando outra análise estatística seria mais pertinente pode levar a resultados errôneos. Por exemplo, se estiver comparando mais de duas médias, a ANOVA seria mais adequada.
Ambiguidade entre Testes Unicaudais e Bicaudais:
- Os testes unicaudais examinam uma direção específica do efeito, enquanto os bicaudais não. Confundir os dois ou usar o tipo errado para a sua pesquisa pode comprometer a validade dos resultados.
Interpretação Errônea de p-valores:
- Um p-valor baixo não significa automaticamente uma diferença significativa na prática, assim como um p-valor alto não indica inexistência de diferença. É essencial interpretar p-valores no contexto do tamanho do efeito, tamanho da amostra e a relevância prática.
Não Considerar o Efeito de Múltiplas Comparações:
- Ao fazer várias comparações com o teste t, o risco de identificar falsos positivos aumenta. Métodos de correção, como o Bonferroni, são essenciais para ajustar e controlar esse risco.
Conclusão
Os testes t desempenham um papel central na pesquisa e na análise de dados, servindo como uma ponte entre amostras e populações, permitindo inferências robustas e decisões informadas.
Estes testes, baseados na estatística t, destacam-se pela sua capacidade de verificar diferenças significativas entre médias, sendo aplicáveis em variados campos, desde a ciência até o mundo dos negócios.
A precisão e confiabilidade do teste t residem em sua aderência a princípios metodológicos rigorosos. Assim, ao aplicar e interpretar corretamente tais testes, os pesquisadores, cientistas e profissionais de diversas áreas conseguem extrair insights valiosos, fundamentando suas conclusões e contribuindo para avanços e descobertas significativas.
Aprofundar o conhecimento sobre os testes t não só potencializa a análise de dados, mas também enriquece nossa capacidade de entender e interpretar o mundo à nossa volta.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Perguntas Frequentes
Q1: O que é a estatística t? É uma ferramenta que mede a diferença entre médias amostrais, levando em conta o desvio padrão e o tamanho da amostra.
Q2: Quando devemos usar o teste t? O teste t é usado para avaliar se há diferenças significativas entre as médias de duas amostras.
Q3: Quando escolher o teste t em vez do teste z? Opte pelo teste t quando a variância da população é desconhecida e o tamanho da amostra é menor que 30.
Q4: O que é p-valor? É uma medida que indica a evidência contra a hipótese nula. Valores baixos sugerem que a diferença é estatisticamente significativa.
Q5: O que significa rejeitar a hipótese nula? Significa que existe evidência suficiente para afirmar que a hipótese inicial provavelmente não é verdadeira.
Q6: Quais são as premissas para realizar um teste t? Independência das observações, dados distribuídos normalmente e homogeneidade das variâncias para testes t de amostras independentes.
Q7: O que ocorre se aplicarmos o teste t sem verificar suas premissas? Podemos obter resultados imprecisos, levando a conclusões incorretas.
Q8: Por que a distribuição t é usada com amostras pequenas? Porque tem caudas mais amplas, o que é adequado para amostras menores onde a variância é menos confiável.
Q9: Como o tamanho da amostra influencia o teste t? Amostras maiores aumentam o poder estatístico, tornando mais fácil detectar diferenças verdadeiras.
Q10: Podemos usar o teste t para mais de duas amostras? Não diretamente. Para mais de duas médias, o ideal é usar a ANOVA.
Baixe GRATUITAMENTE amostras do nosso livro digital!
Aprenda a analisar seus dados com uma metodologia incrível.
O retorno que temos recebido de nossos alunos tem sido excelente!
Clique no link abaixo e saiba mais sobre ele: