Desvendando o Desvio Padrão: Um Guia Prático
Neste artigo você aprenderá os fundamentos do desvio padrão e sua importância na análise de dados, técnicas de interpretação e aplicações práticas.
Em um mundo repleto de variabilidade e incerteza, o desvio padrão surge como um guia confiável — ele representa uma das ferramentas mais usadas e fundamentais em estatística e análise de dados.
Pontos-chave
- O desvio padrão quantifica a variação de um conjunto de dados.
- Outliers podem influenciar significativamente o valor do desvio padrão.
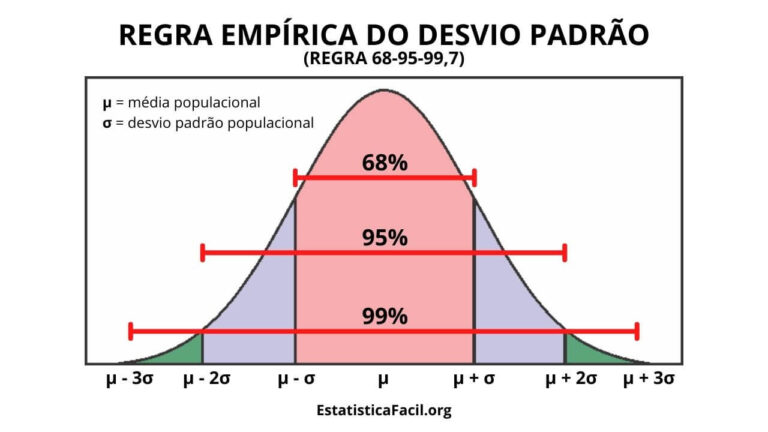
- A regra empírica (68-95-99,7) se aplica a dados com distribuição normal.
- O coeficiente de variação relaciona o desvio padrão à média do conjunto.
- O desvio padrão pressupõe observações independentes e distribuição normal.
O que é o Desvio Padrão?
O desvio padrão é uma medida estatística que quantifica a variação ou dispersão de um conjunto de dados — em outras palavras, ele indica o grau de variação dos valores de um conjunto em relação à sua média.
Esta medida serve para expressar o quão “espalhados” ou “concentrados” estão os dados em um conjunto.
Imagine que você queira saber o quão similares ou distintos são os resultados de um grupo de estudantes em um teste.
O desvio padrão fornece uma resposta quantitativa, esclarecendo se os escores são consistentemente próximos da média ou variam amplamente.
Importância do Desvio Padrão
O Desvio Padrão é uma métrica essencial na estatística e análise de dados, atuando como uma lente pela qual podemos avaliar a consistência e confiabilidade de um conjunto de dados.
Uma das suas funções primárias é permitir a identificação de tendências e padrões significativos, ajudando os pesquisadores a discernir se um padrão é resultado de uma variação aleatória ou se é indicativo de uma tendência subjacente.
Além disso, oferece uma maneira robusta de comparar a variabilidade entre diferentes conjuntos de dados, fornecendo insights sobre a dispersão e centralidade dos pontos de dados em relação às médias.
No mundo das finanças e outros campos que lidam com incertezas, o desvio padrão é inestimável na avaliação de riscos, permitindo que os profissionais prevejam a volatilidade e planejem de acordo.
Ele também é a pedra angular de muitos testes estatísticos, influenciando decisões sobre a validade e confiabilidade dos resultados.
Por último, mas não menos importante, quando os dados são apresentados, seja em pesquisa, negócios ou ciência, o desvio padrão ajuda a contextualizar os resultados, oferecendo uma imagem mais completa da situação em análise.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Aplicações do Desvio Padrão
O Desvio Padrão, pela sua capacidade de quantificar a variabilidade dos dados, encontra aplicação em inúmeros campos e indústrias.
O desvio padrão é usado no setor financeiro para avaliar a volatilidade dos investimentos. Ele ajuda investidores e gestores a comparar a volatilidade de ativos com a média do mercado ou benchmarks. Um desvio padrão elevado pode sinalizar tanto riscos mais altos quanto potencial para maiores retornos.
Em ciências sociais e pesquisa de mercado, o desvio padrão auxilia na análise de dados coletados de pesquisas ou experimentos, destacando variações nas respostas e ajudando a identificar segmentos de população ou comportamentos de consumo.
Na manufatura, é usado para monitorar a qualidade do produto. Processos de fabricação que produzem itens com baixo desvio padrão são considerados confiáveis e consistentes.
Na medicina, ele pode avaliar a eficácia de tratamentos, onde um baixo desvio padrão pode indicar que um tratamento produz resultados consistentes e positivos.
Em meteorologia e análise climática, ajuda a identificar padrões e tendências, fornecendo insights sobre variabilidades climáticas e previsões.
No esporte, treinadores e cientistas do esporte o usam para avaliar o desempenho de atletas, identificando consistência e áreas de melhoria.
Como Calcular o Desvio Padrão
Calcular o desvio padrão pode parecer complexo à primeira vista, mas ao dividir o processo em etapas sequenciais, ele se torna mais compreensível.
| Etapa | Descrição | Procedimento |
|---|---|---|
| 1 | Cálculo da média | Some todos os valores do conjunto e divida pelo número total de valores. |
| 2 | Diferença em relação à média | Subtraia a média de cada valor no conjunto de dados. |
| 3 | Elevar as diferenças ao quadrado | Eleve ao quadrado cada diferença calculada na etapa 2. |
| 4a | (Para populações) Média das diferenças ao quadrado | Some todas as diferenças ao quadrado e divida pelo número de dados. |
| 4b | (Para amostras) Média das diferenças ao quadrado | Some todas as diferenças ao quadrado e divida pelo número de dados - 1. |
| 5 | Cálculo do Desvio Padrão | Extraia a raiz quadrada do resultado da etapa 4a ou 4b. |
Exemplo de Cálculo do Desvio Padrão
Entender o desvio padrão por meio de um exemplo prático é uma abordagem eficaz para consolidar o conceito.
O processo de cálculo pode ser um pouco diferente dependendo se você está lidando com dados de uma população inteira ou apenas uma amostra dessa população.
A seguir, apresentamos um exemplo detalhado, mostrando cada passo do cálculo do desvio padrão para um conjunto de dados.
| Passo | Cálculo | Resultado |
|---|---|---|
| 1 | Calcule a média. Média = (3 + 6 + 9 + 12 + 15) / 5 | Média = 9 |
| 2 | Subtraia a média de cada valor. Diferenças: (3-9), (6-9), (9-9), (12-9), (15-9) | Diferenças: -6, -3, 0, 3, 6 |
| 3 | Eleve as diferenças ao quadrado. Diferenças ao quadrado: (-6)^2, (-3)^2, 0^2, 3^2, 6^2 | Diferenças Quadradas: 36, 9, 0, 9, 36 |
| 4a | (Para populações) Calcule a média das diferenças quadradas. Média das diferenças quadradas = (36 + 9 + 0 + 9 + 36) / 5 | Variância (população) = 18 |
| 4b | (Para amostras) Calcule a média das diferenças quadradas considerando n-1. Média das diferenças quadradas = (36 + 9 + 0 + 9 + 36) / 4 | Variância (amostra) = 22,5 |
| 5 | Obtenha a raiz quadrada da variância. Desvio padrão (população) = √18, Desvio padrão (amostra) = √22,5 | Desvio Padrão (população) ≈ 4,24, Desvio Padrão (amostra) ≈ 4,74 |

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Interpretação do Desvio Padrão
Veja algumas diretrizes para uma interpretação eficaz do desvio padrão:
Medida de dispersão: O desvio padrão evidencia a dispersão dos valores em um conjunto. Quanto maior o desvio padrão, maior a dispersão ou variabilidade dos dados. Já um desvio padrão menor indica que os valores estão mais agrupados em torno da média.
Regra empírica: Para dados que seguem uma distribuição normal, a regra empírica (ou regra 68-95-99,7) é uma ferramenta valiosa. Ela estabelece que cerca de 68% dos dados estão a um desvio padrão da média, 95% a dois desvios padrão, e aproximadamente 99,7% a três desvios padrão.
Identificando outliers: Ao analisar o desvio padrão, é crucial estar atento à presença de outliers. Estes são valores que se distanciam significativamente da média e podem influenciar consideravelmente o desvio padrão. Muitas vezes, é necessário investigar mais profundamente para entender a origem desses outliers.
Interpretação conforme o contexto: A relevância e aceitabilidade do valor do desvio padrão variam conforme o campo de aplicação. Em algumas áreas, um desvio padrão alto pode ser indicativo de maior risco, como nas finanças. Já em processos de controle de qualidade, um desvio padrão baixo é sinônimo de consistência e padronização.
Relativo à média: É importante interpretar o desvio padrão em relação à média do conjunto de dados. Em certos contextos, o coeficiente de variação (CV) — que relaciona o desvio padrão à média — pode ser uma ferramenta útil. O CV, sendo uma medida adimensional, permite comparar a variabilidade entre conjuntos de dados de diferentes magnitudes ou unidades.
Limitações do Desvio Padrão
Relevância da Média: Para que o desvio padrão seja uma medida válida de dispersão, a média do conjunto de dados deve ser a representação adequada do centro dos dados.
Observações Independentes: A correlação ou dependência entre pontos de dados pode distorcer o desvio padrão. Assim, é essencial garantir que as observações sejam independentes para uma análise correta.
Escala de Medição: É crucial reconhecer se os dados estão em uma escala intervalar ou de razão. Essas escalas permitem cálculos de desvio padrão relevantes, ao contrário das escalas nominal e ordinal.
Distribuição Normal dos Dados: Em certos contextos, a aplicação do desvio padrão pressupõe que os dados sejam normalmente distribuídos. A não conformidade com essa distribuição pode levar a interpretações imprecisas.
Considerações Sobre o Desvio Padrão
O desvio padrão é utilizado como uma ferramenta estatística para quantificar a dispersão de um conjunto de dados.
Ele oferece insights valiosos sobre a variabilidade dos dados.
No entanto, é essencial reconhecer suas limitações ao usá-lo como uma métrica de análise:
Incomparabilidade entre Unidades Diferentes: O desvio padrão, sendo uma medida de dispersão, é expresso na mesma unidade que os dados originais. Isso pode tornar difícil a comparação da variabilidade entre conjuntos de dados que têm diferentes unidades de medida.
Desafios na Interpretação: Embora o desvio padrão forneça uma medida quantitativa da dispersão, sua interpretação pode ser desafiadora, especialmente para aqueles que não estão familiarizados com estatísticas. Sem o devido contexto, pode ser difícil discernir se um desvio padrão é considerado alto ou baixo para um determinado conjunto de dados.
Suposição de Distribuição Normal: Em muitos contextos, o desvio padrão é mais relevante quando os dados têm uma distribuição normal. No entanto, nem todos os conjuntos de dados seguem essa distribuição. Quando aplicado a dados que não são normalmente distribuídos, o desvio padrão pode não fornecer uma representação precisa da dispersão.
Alternativas ao Desvio Padrão: Dependendo da natureza e da distribuição dos dados, outras medidas de dispersão, como a amplitude, o intervalo interquartil ou o desvio médio absoluto, podem ser mais apropriadas. Além disso, ferramentas gráficas, como histogramas e box plots, podem complementar o desvio padrão ao oferecer uma visualização mais intuitiva da dispersão dos dados.
Sensibilidade a Outliers: O desvio padrão pode ser significativamente influenciado por outliers ou valores extremos. Um único valor atípico pode distorcer a percepção da dispersão geral de um conjunto de dados. Por exemplo, em um conjunto onde a maioria dos valores está agrupada em torno de uma média, um outlier extremo pode aumentar o desvio padrão, dando a impressão de que os dados são mais dispersos do que realmente são.
Quando Usar o Desvio Padrão
Quantificação da Dispersão: Uma das principais funções do desvio padrão é quantificar o quanto os dados se dispersam em relação à média. Isso permite entender o grau de variabilidade ou consistência em um conjunto de dados.
Dados com Distribuição Normal: Se seus dados seguem uma distribuição normal, o desvio padrão se torna ainda mais relevante, permitindo insights mais precisos sobre a variabilidade dos dados.
Limitações a Considerar: O desvio padrão tem suas restrições. Em dados enviesados ou que não estão em uma escala intervalar, outras medidas de dispersão, como o intervalo interquartil, podem ser mais apropriadas.
Comparando Variabilidade: Em situações onde dois ou mais conjuntos de dados têm médias parecidas, o desvio padrão pode ser uma ferramenta valiosa para comparar a variabilidade entre eles.
Avaliação em Finanças: No campo financeiro, o desvio padrão é frequentemente usado para avaliar riscos ou volatilidade de investimentos. Um desvio padrão mais alto pode indicar um investimento mais arriscado.
Uso Integrado com Outras Ferramentas: O desvio padrão não deve ser a única ferramenta em sua caixa de ferramentas estatísticas. Combiná-lo com outras métricas e técnicas pode proporcionar uma compreensão mais rica e abrangente dos seus dados.
Resumindo
| Tópico | Informação |
|---|---|
| Definição | O desvio padrão avalia a dispersão de um conjunto de valores, quantificando o quão distantes os pontos de dados estão, em média, da média do conjunto. |
| Importância | Ele desempenha um papel vital na análise de dados, permitindo entender a variabilidade dos dados. Auxilia na identificação de tendências, avaliação da confiabilidade dos dados, detecção de valores discrepantes, comparação entre diferentes conjuntos de dados e análise de riscos. |
| Cálculo | Para calcular o desvio padrão, determina-se a média do conjunto, subtrai-se essa média de cada valor, elevam-se estas diferenças ao quadrado, calcula-se a média destas diferenças quadráticas e, finalmente, extrai-se a raiz quadrada deste último valor. |
| Limitações | O desvio padrão tem suas restrições: é sensível a outliers, assume distribuição normal dos dados em determinados contextos, pode não ser comparável entre conjuntos com diferentes unidades e pode apresentar desafios na sua interpretação. |
| Suposições | Ao usar o desvio padrão, é preciso considerar a escala de medida utilizada, garantir que a média é um indicador válido de tendência central, verificar a distribuição dos dados e assegurar que as observações são independentes entre si. |
| Aplicações | Sua aplicação é vasta, incluindo áreas como finanças, indústria, ciências sociais, esportes, medicina e análises climáticas. |
Conclusão
O desvio padrão, sem dúvida, representa uma ferramenta indispensável no universo da análise de dados e estatística.
Sua capacidade de quantificar a dispersão dos dados fornece uma visão crítica sobre a variabilidade, consistência e qualidade das informações em mãos.
Contudo, é imperativo não apenas compreender essa métrica, mas também suas limitações e o contexto em que é empregada.
Cada conjunto de dados carrega sua singularidade e, por isso, o uso integrado do desvio padrão com outras ferramentas estatísticas é essencial para garantir interpretações corretas e apropriadas.
No mundo cada vez mais orientado por dados em que vivemos, desenvolver uma proficiência no entendimento do desvio padrão e suas nuances pode ser o diferencial que separa uma análise superficial de uma análise profunda, significativa e verdadeiramente esclarecedora.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Perguntas Frequentes
Q1: O que é desvio padrão? É uma medida estatística que indica a variação ou dispersão dos valores em um conjunto de dados.
Q2: Como o desvio padrão difere da média? Enquanto a média representa o valor central de um conjunto de dados, o desvio padrão indica quão dispersos os dados estão em relação a essa média.
Q3: O desvio padrão é sempre positivo? Por quê? Sim, porque representa uma distância (dispersão) dos valores e a distância nunca é negativa.
Q4: Como o desvio padrão influencia a tomada de decisões financeiras? Ele ajuda os investidores a entenderem a volatilidade de um ativo e, portanto, os riscos associados ao investimento.
Q5: Em que outros campos o desvio padrão é aplicado? Além das finanças, ele é amplamente usado em medicina, ciência, engenharia e em muitos outros campos de pesquisa.
Q6: Um desvio padrão alto é sempre ruim? Não necessariamente. Um desvio padrão alto indica grande variação nos dados, o que pode ser bom ou ruim, dependendo do contexto.
Q7: Como o desvio padrão se relaciona com a curva de distribuição normal? Em uma distribuição normal, cerca de 68% dos valores estão dentro de um desvio padrão da média. Cerca de 95% estão dentro de dois desvios padrão. E aproximadamente 99,7% estão dentro de três desvios padrão.
Q8: O que é um “desvio padrão populacional”? Refere-se ao desvio padrão de uma população inteira, em contraste com o desvio padrão de uma amostra.
Q9: Por que o desvio padrão é crucial em pesquisas clínicas? Ele permite aos pesquisadores quantificar a variabilidade nos dados, avaliar a confiabilidade dos resultados e comparar a eficácia de diferentes tratamentos.
Q10: É possível ter um desvio padrão de zero? Sim. Isso acontece quando todos os valores em um conjunto de dados são iguais, indicando nenhuma variação.
Baixe GRATUITAMENTE amostras do nosso livro digital!
Aprenda a analisar seus dados com uma metodologia incrível.
O retorno que temos recebido de nossos alunos tem sido excelente!
Clique no link abaixo e saiba mais sobre ele:
ENGLISH VERSION