Tamanho Amostral Para o Teste t: Como Calcular?
Você aprenderá como calcular o tamanho amostral para o Teste t de Student de forma eficiente e prática, otimizando tempo e recursos.
Você sabia que o cálculo do tamanho amostral é um passo importantíssimo de uma análise e que ele economiza seu tempo e dinheiro? Sabia que um tamanho amostral adequado aos seus dados torna seus resultados mais confiáveis?
Apesar disso, muitos pesquisadores coletam e analisam seus dados sem antes se preocupar com este passo, decisão que pode arruinar a confiabilidade dos resultados.
Este passo, apesar de muitas vezes ignorado, é bastante simples! Apresentamos aqui a forma correta de fazer o cálculo do tamanho amostral para o teste t de Student. Melhor ainda, em um excelente programa estatístico gratuito.
O Problema
O principal objetivo do cálculo do tamanho da amostra é determinar o número de participantes necessários para detectarmos um efeito relevante.
Se o tamanho da amostra for muito pequeno, pode não ser possível detectar um efeito existente. Já amostras muito grandes podem gerar perda de tempo, recursos e dinheiro.
Portanto, é importante otimizarmos o tamanho da amostra.
Além disso, o cálculo do tamanho da amostra na fase de projeto do estudo está se tornando cada vez mais um requisito quando se busca a aprovação em comitê de ética para um projeto de pesquisa envolvendo seres humanos ou animais e posterior publicação, por exemplo.
Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Selecione então o teste desejado, teste t para duas amostras independentes. Clique na aba Tests: Means: Two independent groups.
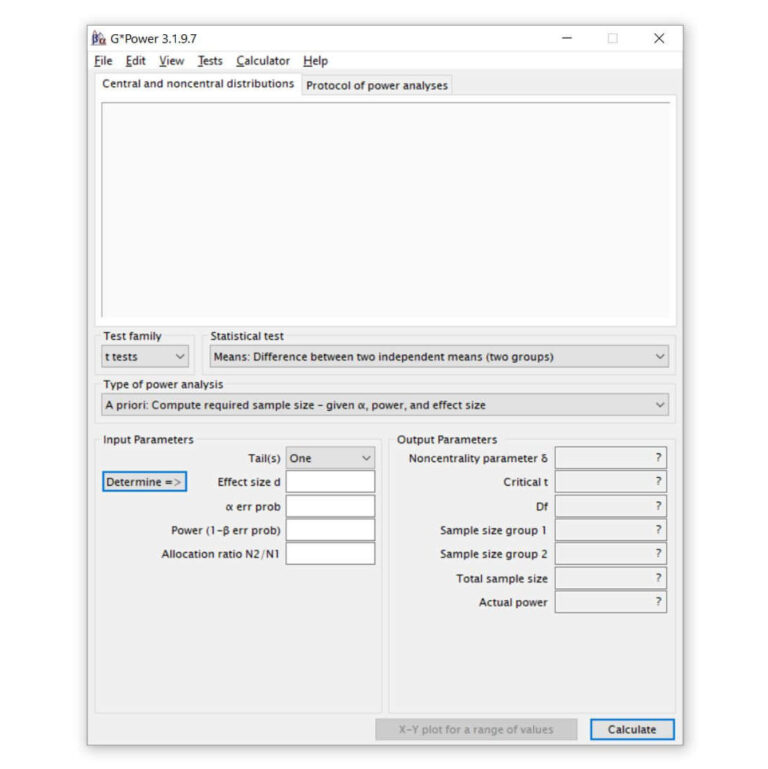
Agora, vamos preencher os campos!
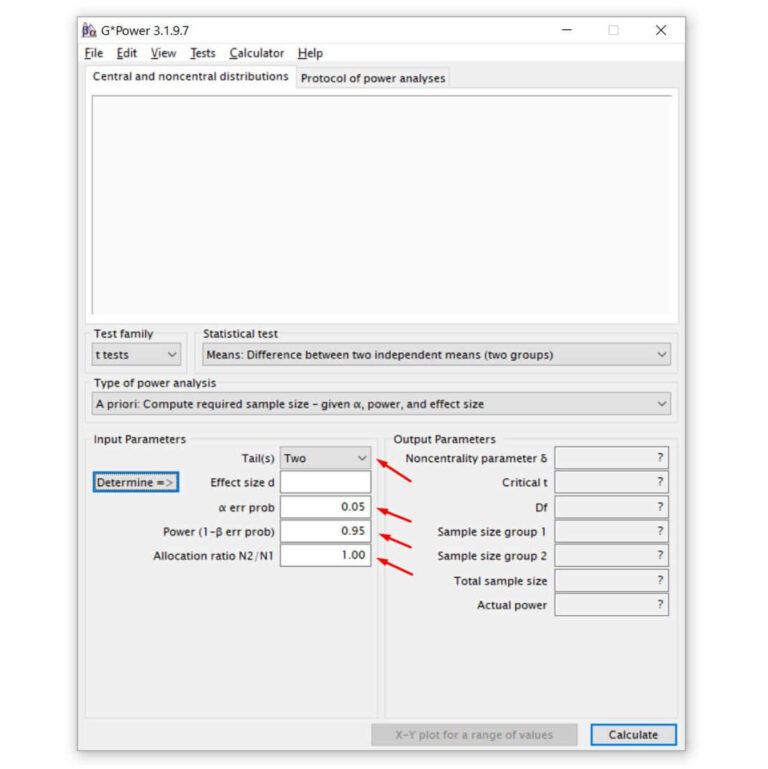
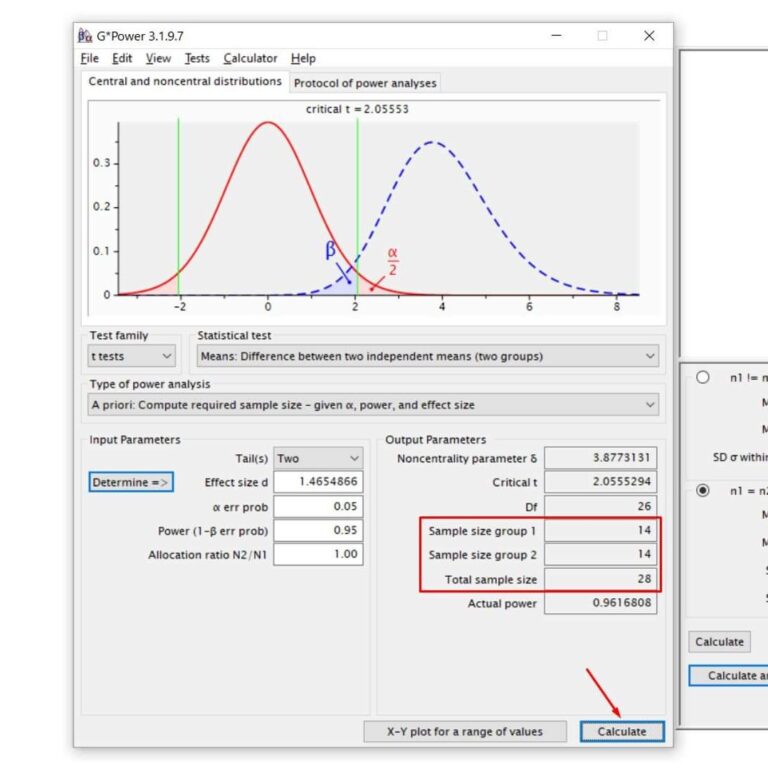
Tail(s) = Cauda(s): Marque One (Um) se o teste for unicaudal ou Two (Dois) se o teste for bicaudal. Mas quando o teste será unicaudal ou bicaudal? Caso a hipótese alternativa seja que a média de um grupo é maior que a média do outro grupo, então usamos o teste unicaudal. Caso a hipótese alternativa seja apenas que as médias são diferentes entre os grupos, sem distinção inicial de qual é maior ou menor, então usamos o teste bicaudal. Essa hipótese deve ser baseada no conhecimento existente na área de estudo. Se não tem certeza, mantenha a opção em Two (Dois).
α err prob = nível de significância: Probabilidade de rejeição da hipótese nula quando ela é verdadeira (erro tipo I). Normalmente os valores utilizados são 0,05 ou 0,01. Um nível de significância de 0,05, por exemplo, indica um risco de 5% de concluir que existe uma diferença quando não há diferença real.
Power (1 – β err prob) = Poder do Teste: Probabilidade de rejeitar a hipótese nula se realmente for falsa, ou seja, o quanto o teste controla o erro tipo II. Normalmente um valor aceitável está entre 0,80 e 0,99. Quanto maior o poder do teste, melhor, mas à medida que o aumentamos, o tamanho amostral requerido também aumenta.
Allocation ratio N2/N1 = Proporção de alocação entre os grupos N2/N1: Caso pretenda que o tamanho amostral dos dois grupos seja o mesmo, então basta entrar com o valor 1. Se quiser outra proporção de alocação entre os grupos, basta entrar com o valor requerido.
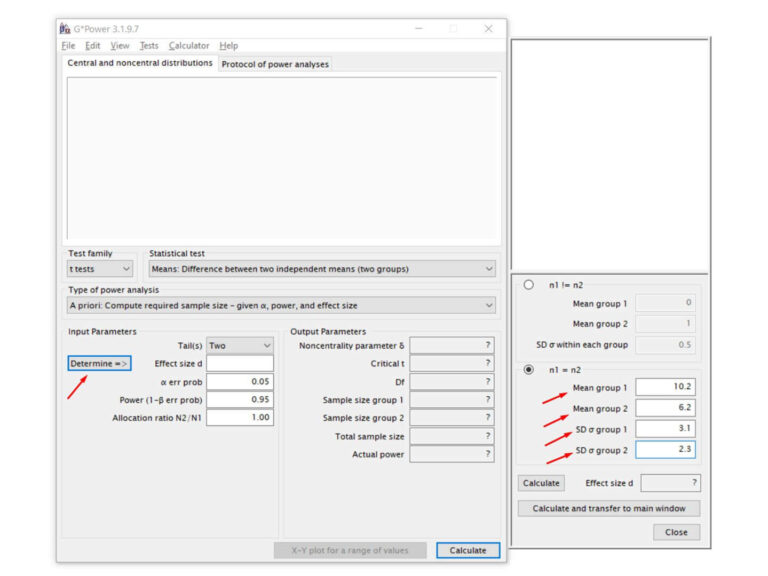
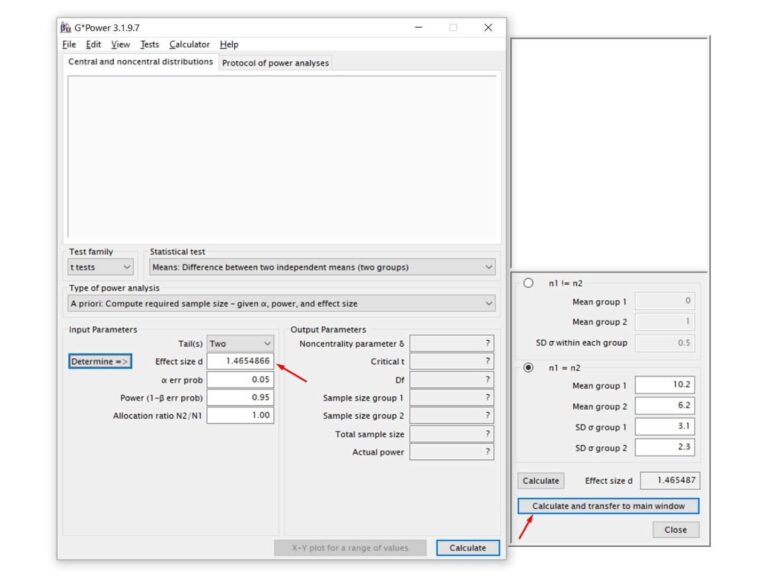
Effect size d = Tamanho do efeito de Cohen (d): Esta medida representa a força da diferença detectada entre os grupos testados. Convencionalmente considera-se d = 0,20 como fraca, d = 0,50 como média, e d = 0,80 como forte. Para definir o d para seu cálculo de tamanho amostral, clique em Determine => (Determinar =>) e uma nova aba vai se abrir. Nesta nova aba precisamos colocar valores da média (Mean) e do desvio padrão (SD σ) dos dois grupos.
Mas se estou na etapa de fazer o cálculo do tamanho amostral para minha amostragem, significa que ainda não coletei e não tenho os dados para calcular a média e desvio padrão, certo?
Para este cálculo você precisa de um valor estimado que pode ser obtido de uma coleta piloto com poucas observações. Estes valores também podem ser obtidos a partir de outros estudos, com populações, espécies ou condições semelhantes ao seu estudo, e até por meio de modelos teóricos.
Agora basta clicar em Calculate and transfer to main windows (Calcular e transferir para a janela principal) que o valor de d estimado para os seus dados será calculado e o campo Effect size d será preenchido.
Para finalizar clique em Calculate (Calcular) e voilà… Agora você tem o tamanho amostral total e dos grupos 1 e 2!
Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Caso queira calcular o tamanho amostral para o teste t para duas amostras dependentes (pareadas), clique na aba Tests: Means: Two dependent groups (matched pairs).
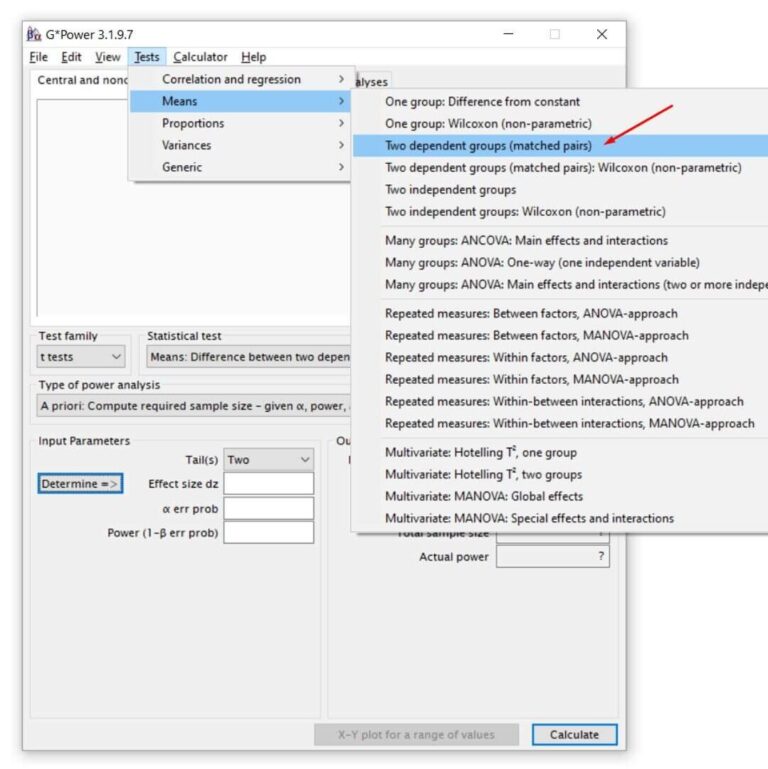
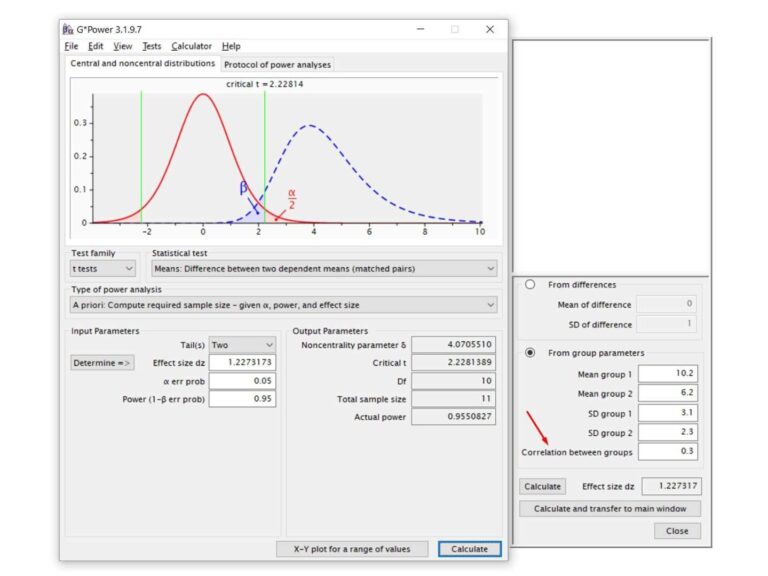
Então, basta preencher os dados exatamente como aprendemos para o teste t para duas amostras independentes. A única diferença é que agora precisamos entrar com um valor de ‘Correlation between groups’ (Correlação entre os grupos). Para obter este valor, basta fazer uma correlação de Pearson entre os dois grupos com os dados da coleta piloto. O valor de r obtido deve ser preenchido ali.
Conclusão
O cálculo do tamanho amostral é um passo bastante simples, mas essencial para que se obtenha resultados mais confiáveis, com economia de tempo e dinheiro.
Para o cálculo precisamos basicamente de alguns dados preliminares referentes aos dois grupos em que busca as diferenças. Estes dados podem ser provenientes de coleta piloto ou até de dados compilados de outros estudos semelhantes.
Agora que já sabe calcular o tamanho amostral para o teste t, você sabe os segredos para fazer um teste t perfeito? Leia este artigo e descubra: Os Segredos do Teste-t.
ATUALIZAÇÃO:
Quer aprender a calcular o tamanho amostral no G*Power para outras análises inferenciais mais importantes?
Então, baixe gratuitamente as amostras do nosso livro digital lançado recentemente.
Lá você aprenderá a calcular o tamanho amostral para o teste t para amostras independentes ou pareadas; anova de uma ou duas vias, para medidas repetidas ou não, e modelo misto; regressão linear e logística simples e múltipla, etc.
Clique neste link e saiba mais sobre ele: Estatística Aplicada: Análise de Dados.
