ANOVA: Não Ignore Esses Segredos
Os segredos da ANOVA residem em suas suposições: independência das observações, normalidade e homocedasticidade. A seleção adequada do tipo de ANOVA, o cálculo preciso do tamanho da amostra e a análise post hoc cuidadosa são cruciais para a obtenção de resultados válidos.
Você sabia que o uso incorreto de análises estatísticas , incluindo a ANOVA, é mais comum do que imaginamos e que isso pode nos levar a tirar conclusões incorretas?
Isto é terrível, pois conclusões incorretas podem levar a tomadas de decisões desastrosas.
Sendo assim, se não deseja que você e suas pesquisas caiam neste buraco, leia este artigo até o final.
O Problema
déjà-vu: forma de ilusão da memória que leva o indivíduo a crer já ter visto (e, por ext., já ter vivido) alguma coisa ou situação de fato desconhecida ou nova para si; paramnésia.
Se parecer que está tendo um déjà-vu enquanto lê este artigo, é porque provavelmente você já leu nosso artigo intitulado “Descubra os segredos do teste t que você não pode ignorar.”
De fato, os dois testes de comparação de médias são muito semelhantes em vários aspectos.
Caso ainda não tenha lido o artigo mencionado acima, ao terminar a leitura deste, abra-o e faça as comparações necessárias. Caso já tenha lido, utilize este de forma comparativa e também como uma revisão.
Assim como no teste t, a ampla disponibilidade e simplicidade, aliadas à facilidade de entendimento e de uso da ANOVA o tornaram um dos testes estatísticos inferenciais mais comumente utilizados no mundo.
Essa “popularização”, no entanto — como acontece com o teste t — acabou trazendo alguns problemas, como o uso incorreto da análise.
Este fato é tão preocupante, que vários artigos de revisão sistemática recentes têm sido feitos — em determinados tipos de estudo, até quase 80% dos artigos publicados apresentam algum tipo de erro nas análises estatísticas!
Como a solução para os problemas da humanidade depende destes estudos, é bastante inquietante pensar que uma proporção tão grande deles foi analisada de forma incorreta e podem como consequência ter levado a conclusões erradas.
Apesar de tudo isso, os “segredos” para se conduzir uma ANOVA de forma correta não é algo complicado ou difícil.
Basta entender algumas características básicas da análise!

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
A Solução
ANOVA significa análise de variância (analysis of variance).
A ANOVA nada mais é que um teste de comparação de médias — basicamente inferindo se as médias de dois ou mais grupos são iguais.
Normalmente a ANOVA é utilizada quando queremos comparar as médias de três ou mais grupos e o teste t quando queremos comparar as médias de somente dois grupos — utilizaremos essa definição aqui.
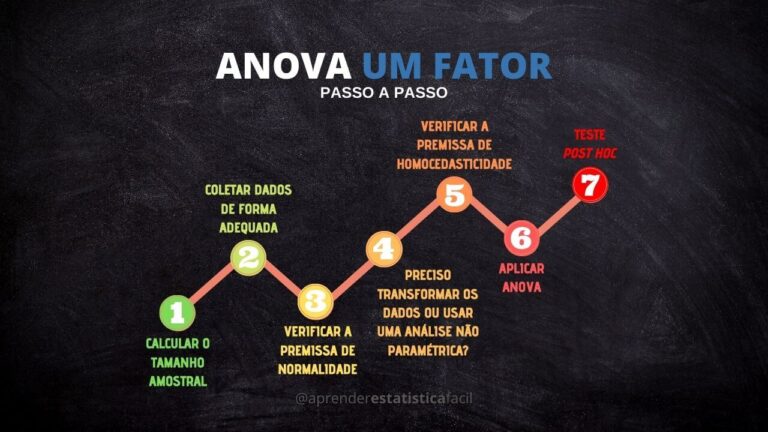
Agora, atente-se, pois, o cumprimento dos seis passos listados a seguir são essenciais para uma aplicação adequada e inquestionável de uma ANOVA.
1. Qual Tipo De ANOVA Devo Usar?
Os tipos principais, mais utilizados, de ANOVA são:
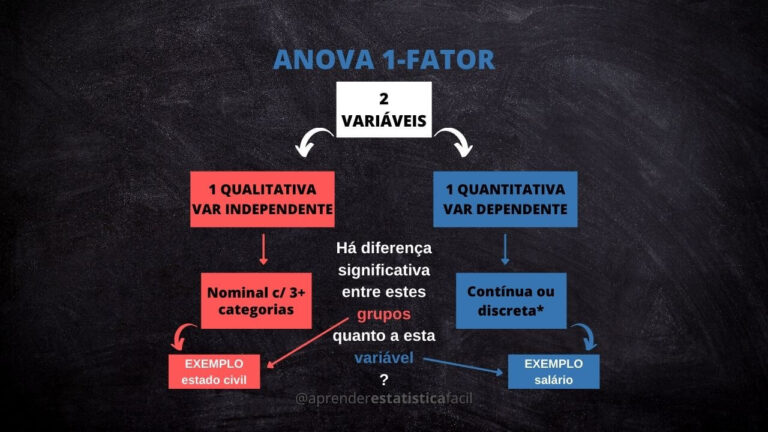
1.1 ANOVA um fator (ou uma via)
Representa o tipo mais comumente utilizado, que verifica se as médias das amostras coletadas de três ou mais grupos são iguais.
De forma mais técnica: verifica o efeito de uma variável categórica independente sob uma variável dependente contínua.
-Por exemplo, quero verificar se as médias da envergadura entre três diferentes espécies de pássaros são iguais ou diferentes.
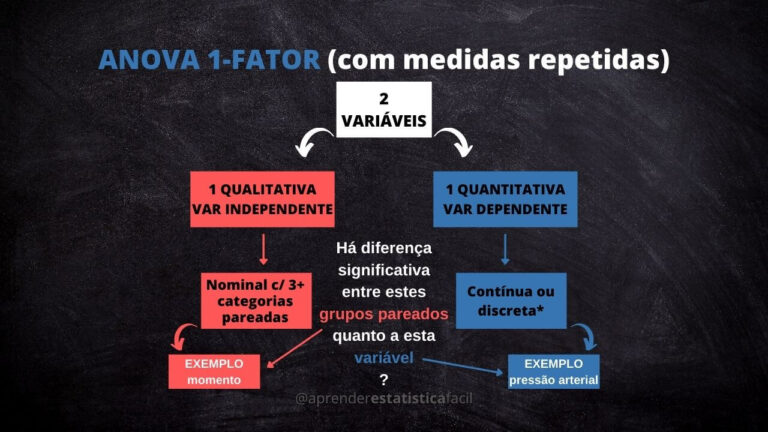
1.2 ANOVA medidas repetidas (um fator)
Este tipo é equivalente à ANOVA um fator, mas neste caso as amostras, entre cada um dos três [ou mais] grupos, são dependentes, ou seja, as amostras são pareadas ou relacionadas.
– Por exemplo, quero verificar se as médias da pressão arterial de mulheres idosas de um município são iguais: (1) uma hora após o uso de um medicamento, (2) duas horas após o uso, e (3) quatro horas após o uso.
– Sendo assim, como a pressão arterial de cada mulher idosa é aferida três vezes — uma hora, duas horas e quatro horas após o uso do medicamento — há o pareamento de cada unidade amostral (cada paciente idosa).
1.3 Outros tipos
Há outros tipos de ANOVA que não serão considerados neste artigo, como a ANOVA dois fatores (ou duas vias) e ANOVA medidas repetidas (dois fatores).
A principal diferença entre as duas é que na ANOVA medidas repetidas as amostras são pareadas.
Estas representam uma extensão da ANOVA um fator, e verificam a influência de duas variáveis categóricas independentes sob uma variável dependente contínua.
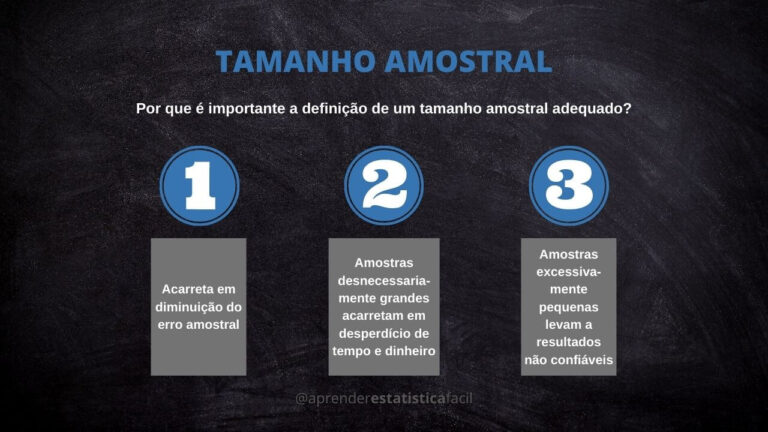
2. Tamanho Amostral
Após a definição de qual tipo ANOVA você vai utilizar, vem o segundo passo: precisamos determinar quantas elementos devemos coletar!
Um tamanho amostral consistente é normalmente a solução de vários dos problemas da estatística.
De forma geral, a melhor maneira de se encontrar o tamanho amostral adequado para nosso teste é por meio de um cálculo específico — para cada teste estatístico há uma diferente.
Para a ANOVA, precisamos da média e do desvio padrão aproximado ou estimado dos grupos estudados.
Com esses dados em mãos, basta entrar com os valores no programa estatístico de cálculo de tamanho da amostra para ANOVA. Então ele retornará o número adequado de elementos que devem ser coletados em cada população.
Mas onde consigo estes dados de média e desvio padrão dos grupos estudados? Normalmente a partir de outros estudos semelhantes ou por meio de coletas piloto!
Verifique este artigo para aprender a calcular o tamanho amostral no teste t!
3. Cada Observação Deve Ser Independente Das Outras!
Na verdade, a independência das observações é uma das premissas mais importantes, e ao mesmo tempo mais ignoradas na estatística.
Não só o teste t, mas TODOS os testes estatísticos dependem desta premissa, que quando violada tende a enviesar a análise e gerar resultados enganosos.
Para que não seja violada, as observações em seu conjunto de dados devem ser independentes, ou seja, cada uma das repetições (ou réplicas) da amostragem não deve apresentar dependência com as outras.
O conceito de aleatoriedade é muito importante aqui. Uma ótima forma de evitar a violação da premissa de independência das observações é coletar seus dados em um universo adequado ao seu estudo e de forma completamente aleatória.
Para entender melhor este conceito, propomos o exemplo a seguir:
Suponha que queremos identificar o perfil genético dos habitantes de um município para responder uma pergunta qualquer.
Após definição do tamanho amostral, uma amostragem aleatória dos indivíduos no município deve ser feita a fim de evitar que a premissa de independência das observações seja violada!
Neste mesmo exemplo, uma forma de amostragem que violaria essa premissa, de forma clara, seria se, para representar um município, amostrássemos somente indivíduos de uma mesma família.
Assim, as observações seriam totalmente dependentes umas das outras, visto que o perfil genético é herdável e apresenta grande semelhança entre familiares.
Pseudo-replicação, que significa “repetição falsa”, é o termo utilizado para definir amostragens que violaram esta premissa.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
4. Normalidade Dos Resíduos
A normalidade dos resíduos representa uma premissa aplicável a todas as análises inferenciais ditas paramétricas.
Esta premissa significa que, para utilização do teste t, seus resíduos devem seguir a famosa distribuição normal, também conhecida como distribuição gaussiana.
Esta distribuição apresenta-se como uma curva em formato de sino, simétrica em torno do seu ponto médio, unimodal.
Mas como devemos fazer para saber se os resíduos se aproximam da distribuição normal?
A boa notícia é que há análises estatísticas denominadas testes de normalidade que identificam esse padrão — dentre os principais estão Shapiro-Wilk, Anderson-Darling e Kolmogorov-Smirnov.
Sempre tome bastante cuidado com a interpretação dos resultados destes testes para não inverter o que ele está realmente indicando.
Caso as análises acima estejam indicando que a premissa de normalidade está sendo violada, há três possibilidades:
(a) Utilizar a Anova mesmo com a premissa violada, alegando que é um teste robusto para estes desvios e que seu tamanho amostral é suficientemente adequado.
(b) Tentar uma transformação dos dados para então uma nova verificação da normalidade.
(c) Por fim, o uso de uma análise não paramétrica análoga ao Anova.
Das três possibilidades, confessamos que da primeira não é de nosso agrado. Afinal de contas, se vai usar o teste t independente do resultado dos testes de normalidade, por qual motivo então estaria fazendo estas análises?
Normalmente fazemos o segundo passo, e caso o problema não seja resolvido, vamos para o terceiro.
Testes parametricos e seus equivalentes não paramétricos:
Anova de um fator = Teste H de Kruskal-Wallis.
Anova de um fator para medidas repetidas = Teste de Friedman
5. Homocedasticidade dos Resíduos
Caso os resíduos não tenham violado a premissa de normalidade, este é o próximo passo.
Apesar do nome grande e estranho, o significado desta premissa é simples de entender.
Homocedasticidade significa nada mais que “variâncias semelhantes”.
Para aplicação da Anova, em sua forma padrão, as variâncias das populações amostradas a serem testadas devem ser semelhantes.
Sendo assim, para verificação se essa premissa, de que as variâncias sejam semelhantes, está sendo violada ou não, existem testes inferenciais nos programas estatísticos!
Dentre os testes mais usados para verificação da igualdade das variâncias estão o teste F, teste de Bartlett e o teste de Levene. No entanto, só faz sentido sua aplicação caso os resíduos não tenham violado premissa de normalidade.
Essa premissa, no entanto, normalmente não representa grande problema, pois se ela estiver sendo violada, ou seja, caso os dados estejam apresentando “variâncias desiguais” (heterocedasticidade), basta utilizar a ANOVA com uma correção (Welch) e, no próximo passo, o teste a posteriori ou post-hoc lidará com isso.
O valor do teste t corrigido para dados com heterocedasticidade, é retornado automaticamente no relatório de resultados da análise na grande maioria dos programas estatísticos.
Só é necessário fazer uma leitura cuidadosa, tanto dos resultados do teste de homocedasticidade dos dados, quanto dos resultados da Anova, com ou sem a correção, para interpretação correta. Por isso atente-se!
6. ANOVA e Testes a posteriori (post hoc)
Caso o teste ANOVA seja significante, a certeza que temos é que há pelo menos um par de médias diferente.
Mas não sabemos qual par, pois, por exemplo, com três grupos temos três possíveis pareamentos, com quatro grupos temos seis possíveis pareamento e assim por diante.
Então, para descobrir qual ou quais pares de médias são diferentes, utilizamos um teste a posteriori (ou post hoc).
Há vários testes a posteriori disponíveis caso a ANOVA seja significante.
Dentre os mais utilizados estão:
1. Assumindo variâncias iguais (homocedasticidade): teste de Tukey (HSD), teste de Bonferroni, teste de Scheffé e teste de Duncan.
2. Não assumindo variâncias iguais (heterocedasticidade): teste de Games-Howell, teste T2 de Tamhane, teste T3 de Dunnet e teste C de Dunnet.
Estes testes post hoc farão as comparações par a par entre todos os grupos e informar entre quais ocorreu diferença significativa.
Conclusão
A ANOVA representa uma das análises estatísticas inferenciais mais utilizadas no mundo.
Vários foram os estudos que a aplicaram de forma incorreta, tornando seus resultados e conclusões no mínimo duvidosos.
Seguindo os seis passos simples que listamos aqui, você tem a possibilidade de executar uma análise inquestionável.
Relembrando, devemos:
[1] escolher o tipo de ANOVA,
[2] definir o tamanho amostral,
[3] fazer a amostragem aleatória adequadamente,
[4] verificar a normalidade dos resíduos,
[5] verificar a igualdade das variâncias, e, por fim,
[6] executar a ANOVA, e então executar seu respectivo teste post hoc.
ATUALIZAÇÃO:
Baixe gratuitamente a amostra do nosso livro digital lançado recentemente.
Nele tratamos detalhadamente dos diferentes tipos de ANOVA.
Tratamos desde o delineamento experimental, com os tipos de amostragem, cálculo de tamanho amostral, análise descritiva, seleção e confecção do gráfico adequado, seleção da análise inferencial adequada e passo a passo ilustrado para sua aplicação respeitando todas as premissas.
Assim, sua análise será inquestionável. Tudo isso com o melhor software estatístico gratuito hoje disponível!
Clique neste link e saiba mais sobre ele: Estatística Aplicada: Análise de Dados.