O que o Desvio Padrão Significa?
O desvio padrão é uma medida que quantifica a variação ou dispersão de um conjunto de dados. Ele indica o quanto os pontos de dados se desviam da média e é especialmente útil quando os dados se ajustam a uma distribuição normal.
Você, que está lendo este artigo, provavelmente já utilizou o desvio padrão pelo menos algumas vezes.
Figura marcada em relatórios, TCCs, dissertações, teses, artigos e etc, o desvio padrão representa uma das medidas-resumo mais utilizadas e ao mesmo tempo incompreendidas e contraintuitivas.
Você saberia dizer o que desvio padrão realmente significa e quando deve utilizá-lo?
O Problema
Os dois principais tipos de estatísticas descritivas são representados pelas medidas de tendência central e as medidas de variabilidade.
Estas medidas, quando usadas em conjunto, representam a base para inúmeras análises, descrições e gráficos na estatística.
A descrição de uma população ou amostra utilizando-se somente uma destas medidas, traz informações incompletas sobre a população, podendo gerar enganos.
Na figura acima, vimos que o uso somente da média para indicar a profundidade do rio, não foi suficiente para evitar o afogamento de uma pessoa.
Uma das lições deixadas por Woody Hayes nesta frase foi exatamente da importância de que uma medida de variabilidade seja utilizada em conjunto com uma medida de tendência central.
Outro exemplo: os três conjuntos de dados apresentados a seguir possuem exatamente a mesma média (20) — mas variabilidades completamente distintas.
A = 20,20,20,20,20
B = 18,19,20,21,22
C = 00,10,20,30,40
Sendo assim, sem uma medida de variabilidade para resumir os dados não conseguiríamos captar estas diferenças essenciais.
As medidas de tendência central, como média aritmética, mediana e moda, são bastante intuitivas, de fácil assimilação.
Já as medidas de variabilidade tendem a ser pouco menos intuitivas de forma geral e, dependendo do tipo, de mais difícil assimilação.
Dentre estas medidas estão a amplitude, o desvio médio absoluto, a variabilidade, o desvio padrão, o coeficiente de variação, além de outras.
Destas, o desvio padrão tem sido a mais utilizada e provavelmente você já o utilizou pelo menos algumas vezes.
O problema é que a grande maioria das pessoas o utilizam sem uma compreensão adequada.
Sendo assim, você saberia dizer o que desvio padrão realmente significa e em quais circunstâncias deveria ser utilizado?

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
A Solução
Alguns exemplos e ideias que usamos aqui, são baseados e foram bem discutidos no livro Estatística [Sem] Matemática, confira neste artigo.
O desvio padrão nada mais é que uma das várias medidas de variabilidade dos dados que existem.
Ele mostra o quanto os dados variam em torno de uma média.
Além do desvio padrão, há outras medidas de variabilidade, mais simples e intuitivas, como a amplitude e o desvio médio absoluto.
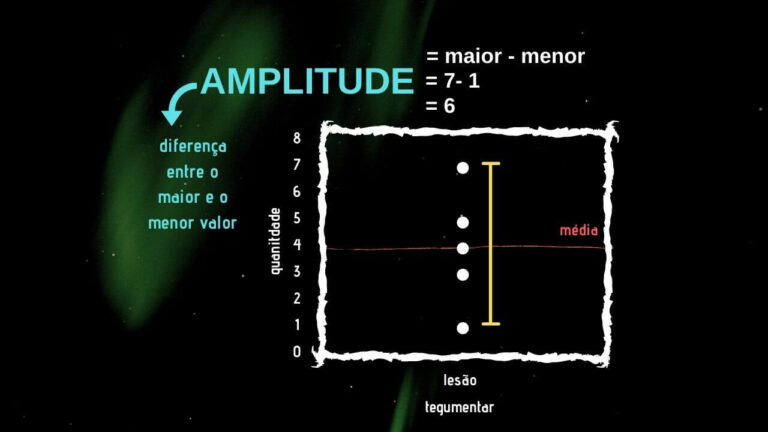
A amplitude é representada pela ‘diferença entre o maior e o menor valor’ do conjunto de dados. Apesar de ser de simples assimilação, tem a desvantagem de somente utilizar dois valores de todo o conjunto de dados.
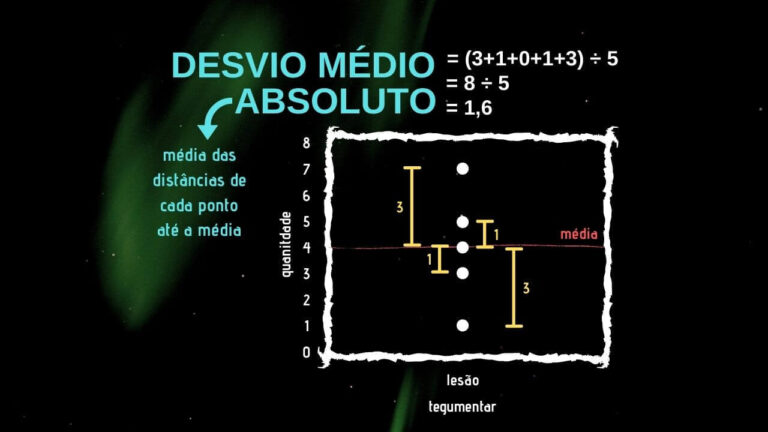
Já o desvio médio absoluto, ou seja, ‘a média das distâncias positivas de cada ponto até a média’, apesar de ser um pouco mais complexo que a amplitude, ainda é bastante intuitivo.
Desvio absoluto = módulo do desvio = desvio positivo
De acordo com Willian Magnusson e Guilherme Mourão, o desvio médio absoluto é tão intuitivo — assim como a média aritmética — que poderíamos esperar que esta fosse a estatística mais utilizada para descrever a variabilidade nos dados. No entanto, ela não é!
A estatística mais utilizada é justamente o “contraintuitivo” desvio padrão, mesmo não sendo completamente entendido pela maioria.
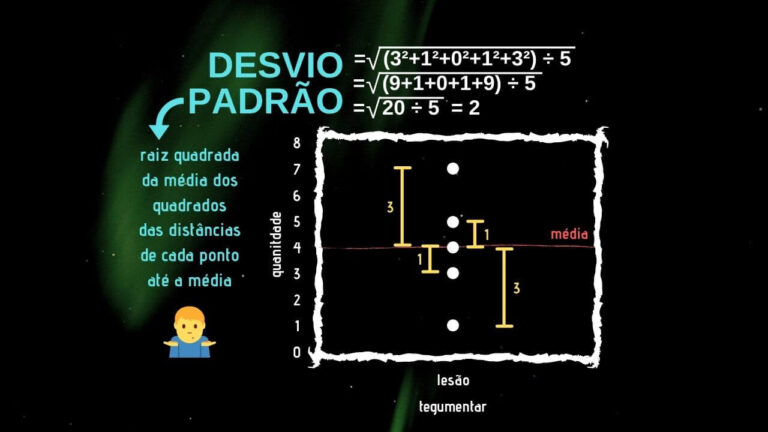
Da mesma forma que o desvio médio absoluto, a obtenção do desvio padrão é baseada nas diferenças do valor de cada observação em relação à média.
No desvio padrão, no entanto, essas diferenças são elevadas ao quadrado, e ao final do processo extrai-se a raiz quadrada.
Com estes exemplos, fica claro que o desvio padrão representa uma medida de variabilidade realmente mais complexa de se entender.
Apesar da subjetiva complexidade, o desvio padrão é muito útil quando os dados analisados seguem a distribuição normal.
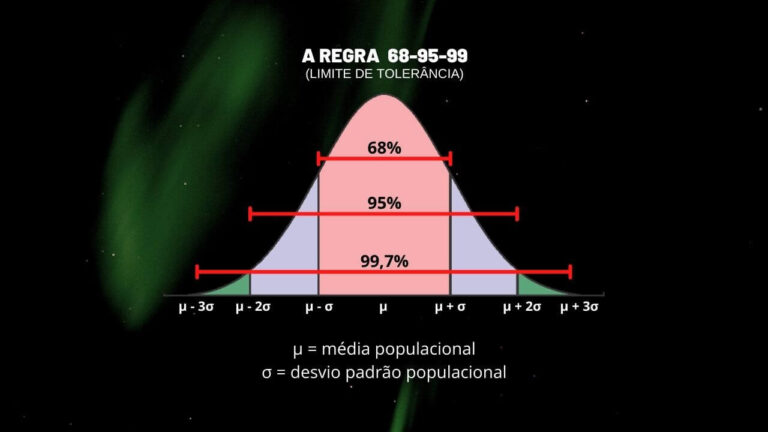
Neste caso, aproximadamente 68% dos valores populacionais estariam compreendidos no intervalo de um desvio padrão; aproximadamente 95% no intervalo de dois desvios padrões; e quase 100% no intervalo de três desvios padrões. Esta regra, 68-95-99, é conhecida como limite de tolerância!
Ronald Fisher já havia argumentado em favor do uso do desvio padrão, mas sob “circunstâncias ideais”, em dados ajustados à distribuição normal.
Sendo assim, de forma geral, caso as circunstâncias não sejam as ideais, com a distribuição não normal, o desvio padrão não teria muita utilidade na descrição da variabilidade.
Na prática, já foi demonstrado que com dados empíricos o desvio médio absoluto teria se saído melhor que o desvio padrão.
Conclusão
O desvio padrão representa uma medida de variabilidade que deve ser utilizada quando os dados seguem perfeitamente a distribuição normal.
O desvio médio absoluto tem se mostrado mais eficaz em estimar a variabilidade de uma população em situações mais realistas, principalmente quando os dados não se ajustam à distribuição normal.
A maior facilidade de entendimento, sua “intuitividade”, e sua melhor eficiência em dados realistas, faz do desvio médio absoluto uma ótima alternativa para representar a variabilidade de grande parte dos dados.
ATUALIZAÇÃO:
Baixe gratuitamente as amostras do nosso livro digital lançado recentemente.
Lá aprenderá mais sobre as medidas-resumo que realmente importam em uma análise de dados.
Fluxogramas para seleção dos testes inferenciais e gráficos adequados, além de passa a passo para todas as análises em software gratuito!
Clique neste link e saiba mais sobre ele: Estatística Aplicada: Análise de Dados.