O que é: Curva de Gauss

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
O que é: Curva de Gauss
A Curva de Gauss, também conhecida como distribuição normal, é um conceito fundamental na estatística e na análise de dados. Ela representa a distribuição de um conjunto de dados em torno de uma média, onde a maioria dos valores se concentra próxima a essa média, e a frequência dos valores diminui à medida que se afastam dela. Essa distribuição é caracterizada por sua forma simétrica e em forma de sino, o que a torna uma ferramenta poderosa para a análise estatística. A Curva de Gauss é amplamente utilizada em diversas áreas, como psicologia, biologia, economia e ciências sociais, para modelar fenômenos naturais e comportamentais.
Características da Curva de Gauss
Uma das principais características da Curva de Gauss é sua simetria em relação à média. Isso significa que, em uma distribuição normal, a média, a mediana e a moda coincidem, ou seja, estão localizadas no mesmo ponto central da curva. Além disso, a curva é definida por dois parâmetros: a média (μ) e o desvio padrão (σ). O desvio padrão é uma medida que indica a dispersão dos dados em relação à média. Quanto maior o desvio padrão, mais espalhados estarão os dados, resultando em uma curva mais larga. Por outro lado, um desvio padrão menor indica que os dados estão mais concentrados em torno da média, resultando em uma curva mais estreita.
Propriedades Estatísticas da Curva de Gauss
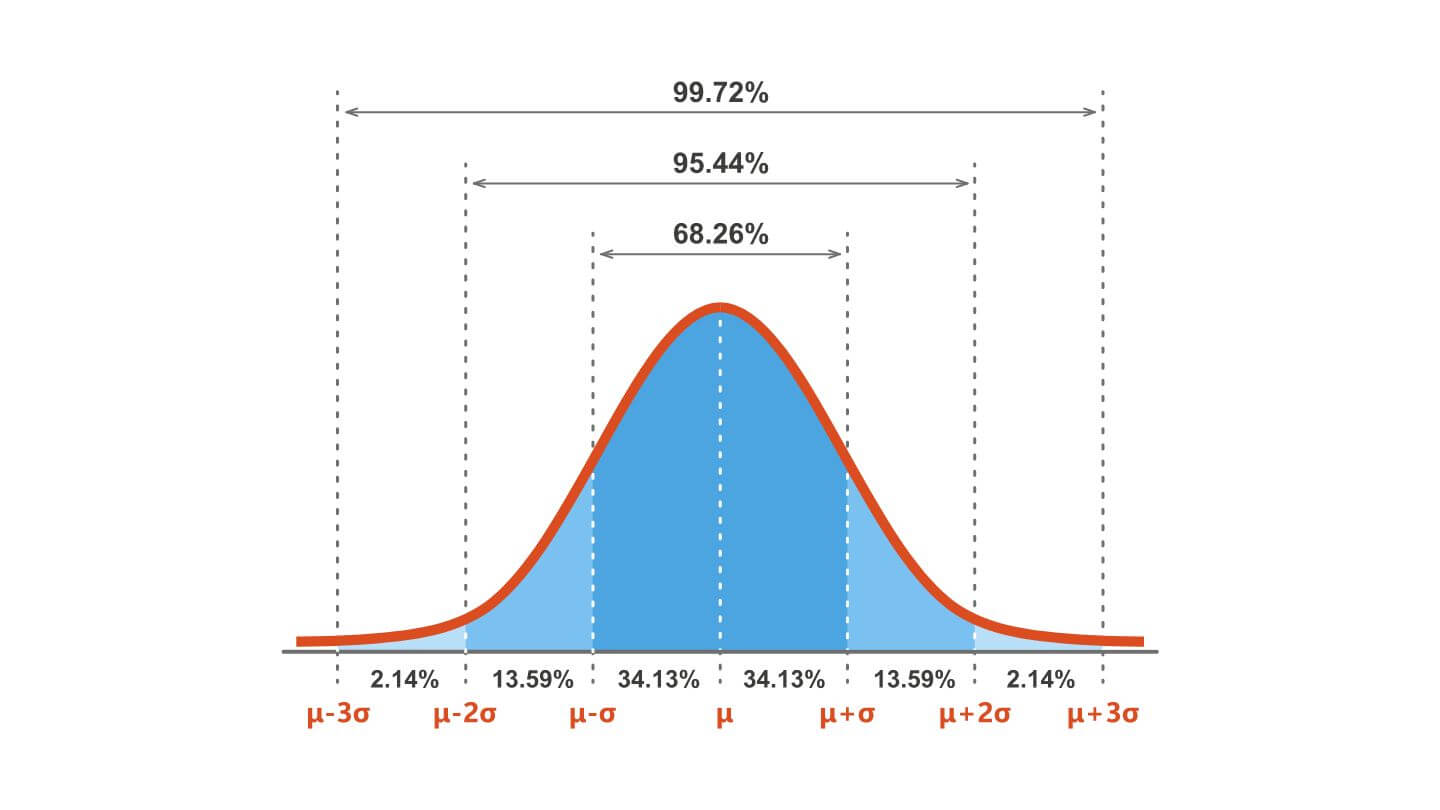
A Curva de Gauss possui várias propriedades estatísticas que a tornam útil para a análise de dados. Uma delas é a regra empírica, que afirma que aproximadamente 68% dos dados em uma distribuição normal estão dentro de um desvio padrão da média, cerca de 95% estão dentro de dois desvios padrão e cerca de 99,7% estão dentro de três desvios padrão. Essa propriedade é fundamental para a realização de inferências estatísticas e para a construção de intervalos de confiança. Além disso, a Curva de Gauss é utilizada para calcular probabilidades, permitindo que os analistas determinem a probabilidade de um determinado evento ocorrer dentro de um intervalo específico.
Aplicações da Curva de Gauss
As aplicações da Curva de Gauss são vastas e variadas. Na área da psicologia, por exemplo, ela é utilizada para analisar testes de inteligência, onde os resultados tendem a seguir uma distribuição normal. Na biologia, a Curva de Gauss é aplicada para modelar características fenotípicas, como altura e peso, que geralmente se distribuem de forma normal em uma população. Na economia, a distribuição normal é frequentemente utilizada para modelar o retorno de investimentos e a volatilidade do mercado. Essas aplicações demonstram a versatilidade da Curva de Gauss em diferentes campos do conhecimento.

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Importância da Curva de Gauss na Ciência de Dados
Na ciência de dados, a Curva de Gauss desempenha um papel crucial na análise exploratória de dados e na modelagem preditiva. Muitos algoritmos de aprendizado de máquina assumem que os dados seguem uma distribuição normal, o que facilita a aplicação de técnicas estatísticas e a interpretação dos resultados. Além disso, a normalização dos dados, que envolve a transformação de variáveis para que sigam uma distribuição normal, é uma prática comum em pré-processamento de dados. Essa normalização é essencial para melhorar a performance de modelos e garantir que os resultados sejam mais robustos e confiáveis.
Limitações da Curva de Gauss
Apesar de suas amplas aplicações, a Curva de Gauss não é isenta de limitações. Nem todos os conjuntos de dados seguem uma distribuição normal, e a aplicação inadequada da Curva de Gauss em dados que não são normalmente distribuídos pode levar a conclusões errôneas. Por exemplo, dados com assimetria ou com outliers significativos podem distorcer a análise. Portanto, é fundamental que os analistas realizem testes de normalidade, como o teste de Shapiro-Wilk ou o teste de Kolmogorov-Smirnov, antes de aplicar técnicas que assumem a normalidade dos dados.
Visualização da Curva de Gauss
A visualização da Curva de Gauss é uma prática comum em estatística e ciência de dados. Gráficos de densidade e histogramas são frequentemente utilizados para representar a distribuição dos dados e verificar se eles seguem uma distribuição normal. A representação gráfica da Curva de Gauss permite que os analistas identifiquem visualmente a média, o desvio padrão e a dispersão dos dados. Além disso, a visualização ajuda na comunicação dos resultados para públicos não técnicos, facilitando a compreensão dos conceitos estatísticos envolvidos.
Relação com Outras Distribuições
A Curva de Gauss é apenas uma das várias distribuições estatísticas existentes. Outras distribuições, como a distribuição binomial, a distribuição de Poisson e a distribuição exponencial, têm características e aplicações distintas. No entanto, a Curva de Gauss é frequentemente utilizada como uma referência devido à sua ubiquidade em fenômenos naturais e sociais. Além disso, o Teorema Central do Limite afirma que, sob certas condições, a soma de variáveis aleatórias independentes tende a se distribuir normalmente, independentemente da distribuição original das variáveis. Isso reforça a importância da Curva de Gauss na teoria da probabilidade e na estatística.
Conclusão sobre a Curva de Gauss
A Curva de Gauss é um conceito central na estatística e na análise de dados, com aplicações que vão desde a psicologia até a economia. Sua forma simétrica e suas propriedades estatísticas a tornam uma ferramenta valiosa para a modelagem e a interpretação de dados. Embora tenha suas limitações, a Curva de Gauss continua a ser um pilar fundamental na análise estatística, permitindo que os analistas façam inferências e tomem decisões informadas com base em dados.
Perguntas Frequentes sobre Curva de Gauss
O que diz a Curva de Gauss?
A Curva de Gauss, ou distribuição normal, descreve a distribuição dos dados em torno de uma média. Ela segue um padrão simétrico em forma de sino, onde a maioria dos valores se concentra próximo à média e se torna menos frequente à medida que se afasta dela.
Para que serve a Gaussiana?
A Gaussiana é utilizada para modelar fenômenos naturais e sociais, prever tendências e calcular probabilidades. Ela é aplicada em áreas como psicologia, biologia, economia e engenharia, sendo uma ferramenta essencial na estatística e na ciência de dados.
Como calcular a Curva Gaussiana?
A Curva Gaussiana segue a função de densidade da distribuição normal, expressa pela fórmula: f(x) = (1 / (σ * sqrt(2 * π))) * exp(-((x - μ)^2) / (2 * σ^2)) onde μ representa a média dos dados, σ é o desvio padrão e x é o valor da variável aleatória. Para calcular a curva, basta substituir os valores da média e do desvio padrão e aplicar a função exponencial.
Como ler a curva da distribuição normal?
A leitura da Curva de Gauss se baseia na posição da média, que é o ponto central da distribuição. De acordo com a regra empírica, aproximadamente 68% dos valores estão dentro de um desvio padrão da média, 95% dentro de dois desvios padrão e 99,7% dentro de três desvios padrão. Essa regra ajuda a entender a dispersão dos dados em torno da média.
Qual é a teoria de Gauss?
Carl Friedrich Gauss formulou diversos conceitos matemáticos e estatísticos, incluindo a distribuição normal. A teoria de Gauss na estatística está relacionada à distribuição de erros em medições e ao conceito de probabilidade normal, que modela muitos fenômenos naturais
Como saber se a distribuição é normal?
Para verificar se um conjunto de dados segue uma distribuição normal, podem ser usados testes estatísticos como o teste de Shapiro-Wilk, o teste de Kolmogorov-Smirnov e o teste de Anderson-Darling. Além disso, histogramas e gráficos QQ-plot ajudam a visualizar a normalidade dos dados.
Como funciona o Gauss?
Carl Friedrich Gauss foi um matemático que fez contribuições fundamentais para diversas áreas, incluindo álgebra, geometria e estatística. Seu trabalho na distribuição normal ajudou a modelar a dispersão de dados e desenvolver métodos estatísticos amplamente utilizados até hoje.
Para que serve a integral gaussiana?
A integral gaussiana é utilizada para calcular probabilidades dentro de uma distribuição normal. Como a integral da função da curva gaussiana não tem uma solução exata em termos de funções elementares, os cálculos são feitos por meio de tabelas estatísticas ou computacionalmente.
Quando podemos usar a Lei de Gauss?
A Lei de Gauss pode se referir a diferentes conceitos matemáticos e físicos. Na estatística, a distribuição normal é usada quando os dados apresentam um comportamento aleatório que se agrupa em torno da média, permitindo previsões baseadas na teoria da probabilidade.
O que é escala de Gauss?
O termo "escala de Gauss" não é um conceito estatístico formal, mas pode estar relacionado à distribuição normal padronizada, onde os dados são transformados para que tenham uma média igual a zero e um desvio padrão igual a um. Esse processo facilita a comparação entre diferentes conjuntos de dados e é útil para métodos estatísticos que exigem normalização.
Qual é a relação entre a Curva de Gauss e o Teorema Central do Limite?
O Teorema Central do Limite afirma que, independentemente da distribuição original dos dados, a soma ou média de um grande número de variáveis aleatórias independentes tenderá a seguir uma distribuição normal. Isso explica por que a Curva de Gauss aparece frequentemente em diversos fenômenos naturais e sociais.
O que significa a simetria da Curva de Gauss?
A simetria da Curva de Gauss significa que a distribuição tem um formato espelhado em relação à média. Isso implica que a média, a mediana e a moda são iguais e estão localizadas no centro da distribuição, dividindo a curva em duas metades idênticas.
O que acontece quando o desvio padrão aumenta ou diminui?
Quando o desvio padrão aumenta, a curva se torna mais achatada e larga, indicando maior dispersão dos dados. Quando o desvio padrão diminui, a curva se torna mais estreita e alta, indicando que os valores estão mais concentrados próximos à média.
Por que a distribuição normal é importante para testes estatísticos?
Muitos testes estatísticos, como o teste t, ANOVA e regressão linear, assumem que os dados seguem uma distribuição normal. Isso permite o uso de inferências estatísticas confiáveis, pois a distribuição normal tem propriedades bem estabelecidas que facilitam os cálculos de probabilidade.
Quais são as principais aplicações da Curva de Gauss na ciência de dados?
Na ciência de dados, a Curva de Gauss é amplamente usada na normalização de dados, modelagem estatística, aprendizado de máquina e análise preditiva. Muitos algoritmos estatísticos assumem que os dados seguem uma distribuição normal para otimizar cálculos e previsões.
A Curva de Gauss pode ser aplicada a qualquer conjunto de dados?
Não. Nem todos os conjuntos de dados seguem uma distribuição normal. Antes de aplicar métodos estatísticos baseados na Curva de Gauss, é essencial testar a normalidade dos dados. Para dados assimétricos ou com outliers, outras distribuições podem ser mais apropriadas.
Como visualizar a Curva de Gauss em um conjunto de dados?
A distribuição normal pode ser visualizada por meio de histogramas, gráficos de densidade e QQ-plots. Essas representações gráficas ajudam a verificar se os dados seguem um padrão simétrico e próximo ao formato esperado da Curva de Gauss.
Qual a relação entre a distribuição normal e a distribuição binomial?
Quando o número de tentativas em uma distribuição binomial é grande e a probabilidade de sucesso não é extremamente baixa ou alta, a distribuição binomial pode ser aproximada por uma distribuição normal. Isso facilita cálculos probabilísticos em amostras grandes.
O que fazer quando os dados não seguem uma distribuição normal?
Se os dados não seguem uma distribuição normal, podem ser aplicadas transformações matemáticas, como a transformação de Box-Cox ou logaritmo, para aproximá-los de uma distribuição normal. Caso isso não seja possível, pode-se utilizar testes estatísticos não paramétricos, que não assumem normalidade.
Quais distribuições estatísticas são alternativas à Curva de Gauss?
Algumas distribuições estatísticas que podem ser utilizadas como alternativas à distribuição normal incluem a distribuição de Poisson (para contagens de eventos), a distribuição exponencial (para tempos de espera entre eventos) e a distribuição t de Student (para pequenas amostras).

Título do Anúncio
Descrição do anúncio. Lorem ipsum dolor sit amet, consectetur adipiscing elit.