ANOVA de Um Fator: Um Guia Completo para Iniciantes

Você aprenderá os passos para conduzir uma ANOVA de um fator para comparar médias de grupos.

A Análise de Variância (ANOVA) de um fator é uma ferramenta estatística utilizada para testar as diferenças entre as médias de três ou mais grupos independentes. Ela ajuda a determinar se existe uma diferença significativa entre as médias dos grupos ou se as diferenças são devido a variação aleatória (acaso). Essa análise é chamada de ANOVA de “um fator” porque considera apenas uma variável independente (fator) com múltiplas categorias (grupos) e examina o impacto deste fator em uma única variável dependente contínua. O teste compara a variabilidade dentro de cada grupo com a variabilidade entre os grupos. Se a variabilidade entre os grupos for significativamente maior que a variabilidade dentro dos grupos, então, pode haver uma diferença nas médias dos grupos comparados.

Pontos-chave

O ANOVA de um fator compara as médias de 3 ou mais grupos para determinar diferenças significativas.
Você deve verificar a normalidade e a homogeneidade das variâncias antes de realizar a ANOVA de um fator.
Os testes de Shapiro-Wilk e Kolmogorov-Smirnov ajudam a verificar a normalidade dos resíduos (erros).
Os testes de Levene e Bartlett ajudam a confirmar a homogeneidade das variâncias.
Em caso de resultados significativos, use testes post hoc apropriados como o teste de Tukey HSD, Bonferroni ou o teste de Scheffe.

Variáveis Necessárias para a
ANOVA de Um Fator

Para realizar uma ANOVA de um fator, você precisará de dois tipos de variáveis: uma variável independente qualitativa com três ou mais grupos e uma variável dependente quantitativa contínua.

Variável independente qualitativa (fator): Representa categorias ou grupos distintos que você deseja comparar. Essas categorias podem ser diferentes tratamentos, intervenções ou outros agrupamentos dentro do seu estudo.

Variável dependente quantitativa contínua: Representa o resultado ou resposta que você medirá e comparará entre os diferentes grupos. Esta variável deve ser contínua, significando que pode assumir qualquer valor dentro de um determinado intervalo. Ela deve ser medida em uma escala de intervalo ou razão para atender às premissas da ANOVA de um fator.

Analisando a relação entre essas duas variáveis, você pode determinar se as diferenças nas médias da variável dependente entre os grupos são estatisticamente significativas.

Premissas da ANOVA de Um Fator

A ANOVA de um fator depende que certas premissas sejam atendidas para que o teste produza resultados válidos. Essas premissas são:

Independência das observações: As observações dentro e entre os grupos devem ser independentes umas das outras. Isso significa que a amostragem de dados deve ser aleatória e não influenciada por fatores externos ou relações entre os sujeitos. Essa premissa é atendida quando fazemos um bom delineamento amostral, com a obtenção de amostras completamente aleatórias.

Normalidade: A distribuição dos resíduos (erros) deve ser aproximadamente normal. Esta premissa pode ser verificada usando vários métodos, como histogramas, gráficos Q-Q ou testes estatísticos como o de Shapiro-Wilk ou Kolmogorov-Smirnov.

Homogeneidade das variâncias: As variâncias dos resíduos (erros) devem ser aproximadamente iguais em todos os níveis da variável independente. Isso também é conhecido como a premissa de homocedasticidade. Você pode usar os testes de Levene ou Bartlett para verificar a homogeneidade das variâncias.

Os resultados da ANOVA de um fator podem não ser confiáveis caso essas premissas forem violadas.

Para violação da premissa de normalidade, uma solução seria a transformação dos dados ou usar uma alternativa não paramétricas como o teste de Kruskal-Wallis, que não requer as mesmas premissas que a ANOVA de um fator.

Em caso de violação da premissa de homocedasticidade, você pode usar a correção de Welch, que é robusta a violações dessa premissa.

Dados de Exemplo

Suponha que queremos comparar os efeitos de três diferentes métodos de ensino nos resultados de testes dos alunos. Assim, temos três grupos de alunos, cada um ensinado por um método diferente:

Grupo 1: Ensino tradicional em sala de aula (aulas e livros didáticos)
Grupo 2: Aprendizado online (videoaulas e recursos online)
Grupo 3: Aprendizado híbrido (uma mistura de ensino tradicional e online)

Coletaremos as notas de testes de 10 alunos em cada grupo. Aqui estão os dados de amostra:

Copiar Dados para Área de Transferência

Método de Ensino	Pontuação
Método A	75,2
Método A	80,5
Método A	82,4
Método A	76,1
Método A	84,3
Método A	88,6
Método A	90,8
Método A	70,7
Método A	85,9
Método A	89,4
Método B	78,6
Método B	81,3
Método B	74,7
Método B	87,2
Método B	83,5
Método B	80,9
Método B	88,4
Método B	85,0
Método B	86,1
Método B	92,8
Método C	90,1
Método C	94,2
Método C	92,6
Método C	85,8
Método C	89,1
Método C	91,3
Método C	88,7
Método C	84,5
Método C	95,4
Método C	86,3

ANOVA de Um Fator Passo a Passo

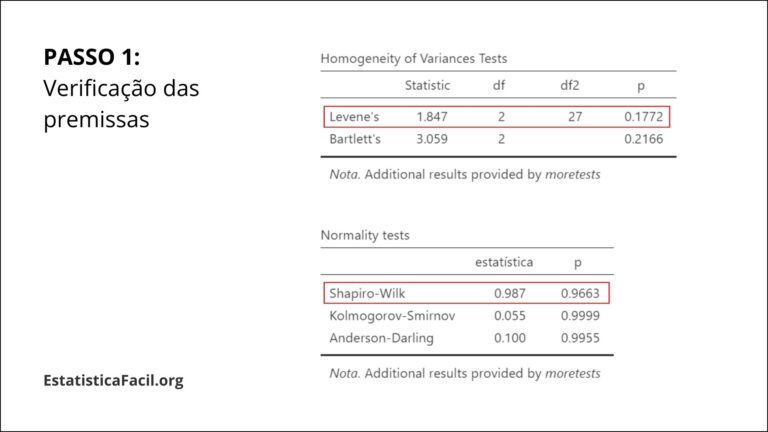
PASSO 1

Verificação das Premissas

Realize testes estatísticos para verificar as premissas, como os testes de Shapiro-Wilk ou Kolmogorov-Smirnov para normalidade e os testes de Levene ou Bartlett para homogeneidade das variâncias.

Se o valor de p para o teste de normalidade for menor que um nível de significância pré-determinado (por exemplo, 0,05), isso indica que os resíduos (erros) não seguem uma distribuição normal, violando assim a premissa de normalidade.

Se o valor de p para o teste de homocedasticidade for menor que um nível de significância pré-determinado (por exemplo, 0,05), isso indica que os resíduos (erros) não apresentam variâncias homogêneas, violando assim a premissa de homocedasticidade.

Se a premissa de normalidade não for atendida, considere transformar os dados ou usar o método estatístico alternativo não paramétrico teste de Kruskal-Wallis. Mas se a premissa violada for a de homoscedasticidade, considere utilizar a ANOVA com correção de Welch.

PASSO 2

Resultados da ANOVA

Realize agora a ANOVA de um fator para comparar as médias dos três grupos.

Verifique o valor de p do teste F para determinar se existe uma diferença significativa entre as médias dos grupos. Se o valor de p for menor que o nível de significância pré-determinado (por exemplo, 0,05), conclua que há uma diferença significativa entre os grupos.

Calcule e informe a medida de tamanho do efeito, como eta-quadrado (η²) ou ômega-quadrado (ω²), para estimar a magnitude das diferenças entre as médias dos grupos.

Assim, é importante que seja reportado o valor de F, os graus de liberdade, o valor de p e a medida de tamanho de efeito.

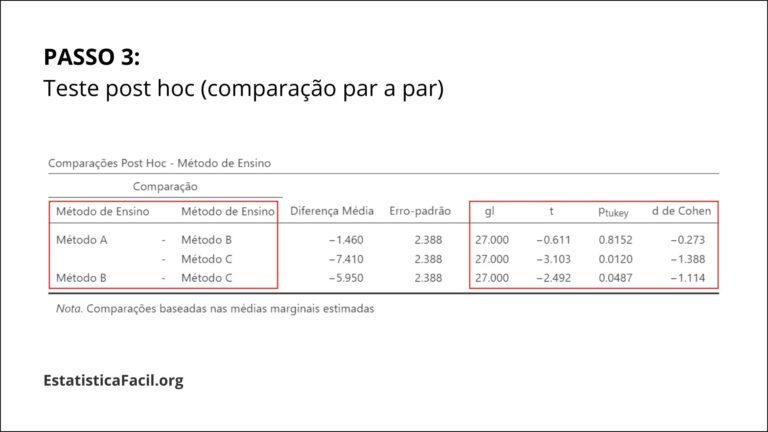
PASSO 3

Teste Post Hoc

Se os resultados da ANOVA de um fator forem significativos, realize testes post hoc para identificar os pares específicos de grupos com diferenças significativas em suas médias.

Escolha um teste post hoc apropriado com base nos dados e premissas (por exemplo, teste de Tukey HSD para dados com homocedasticidade e Games-Howell para dados com heterocedasticidade).

Por fim, para cada comparação do teste post hoc, informe o valor de t, grau de liberdade, valor de p e tamanho de efeito d de Cohen. Por exemplo, o Método C foi superior ao Método A (t(27) = -3,103, p = 0,0120, d = -1,388).

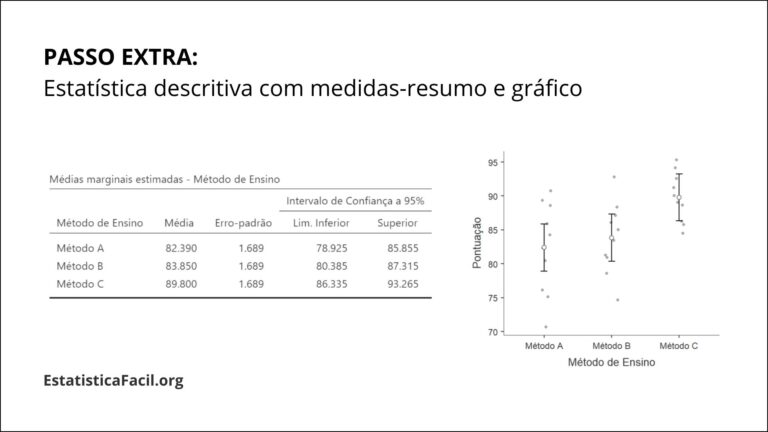
EXTRA

Estatística Descritiva

Crie representações gráficas dos dados, como gráficos de caixa (box plot) ou gráficos de média com barra de erros, para visualizar as diferenças entre as médias dos grupos.

Você pode também apresentar estatísticas descritivas como medidas-resumidas (por exemplo, média, desvio padrão) para cada grupo, a fim de compreendermos mais claramente os dados.

Interprete então os resultados no contexto da questão de pesquisa e discuta as implicações práticas dos achados.

Seguindo esses passos, você poderá conduzir uma ANOVA de um fator correta, de forma a fornecer insights significativos sobre as diferenças entre os grupos em estudo.

Erros Comuns

Evitar erros comuns na ANOVA de um fator é essencial para obtermos resultados precisos e confiáveis.

Isso inclui verificar e atender às premissas de normalidade e homogeneidade das variâncias e ser cauteloso ao interpretar resultados não significativos, considerando o contexto, tamanho da amostra e poder estatístico.

É essencial escolher o teste post hoc correto com base nos dados e premissas e considerar o tamanho do efeito e a significância prática ao lado dos valores de p.

Quando as premissas forem violadas, considere usar transformações de dados, métodos de correção ou testes não paramétricos.

Além disso, informe consistentemente as estatísticas descritivas como média e desvio padrão para cada grupo e visualize os dados usando gráficos de caixa ou gráficos de barras para apoiar e aprimorar a interpretação.

Assim, você poderá fornecer insights significativos sobre as diferenças entre os grupos em estudo.

Conclusão

A ANOVA de um fator é uma ferramenta estatística poderosa para comparar as médias de três ou mais grupos e determinar se há diferenças significativas entre eles. Ao considerar cuidadosamente as premissas, interpretar os resultados de forma correta e evitar erros comuns, você pode extrair conclusões significativas de seus dados e contribuir com insights valiosos para sua área de estudo. Discutimos a importância de verificar as premissas, escolher os testes post hoc apropriados e considerar a significância estatística e prática dos achados. Também destacamos o valor de relatar estatísticas descritivas e visualizar os dados para compreender completamente os resultados.

Ao conduzir análises de ANOVA de um fator em sua pesquisa, lembre-se sempre de:

1. Verificar as premissas e tratar quaisquer violações.

2. Realizar a análise com cuidado, considerando tanto os valores de p quanto os tamanhos de efeito.

3. Usar testes post hoc apropriados para identificar diferenças específicas entre os grupos.

4. Relatar estatísticas descritivas e visualizar os dados por meio de gráficos para apoiar suas conclusões.

Seguir estas diretrizes permitirá que você conduza uma ANOVA de um fator completa e contribua com conhecimento para sua área.

Artigos Recomendados

Perguntas Frequentes

P1: O que é ANOVA de um fator? ANOVA de um fator é uma ferramenta estatística usada para testar as diferenças entre as médias de três ou mais grupos independentes. Ajuda a determinar se há uma diferença significativa entre as médias ou se as diferenças são devido a variação aleatória.

P2: Quais são as premissas da ANOVA de um fator? As premissas da ANOVA de um fator são independência das observações, normalidade dos resíduos (erros) e homogeneidade das variâncias.

P3: Como verifico as premissas para a ANOVA de um fator? Você pode verificar a normalidade usando histogramas, gráficos Q-Q ou testes como Shapiro-Wilk ou Kolmogorov-Smirnov. A homogeneidade das variâncias pode ser verificada usando os testes de Levene ou Bartlett.

P4: O que devo fazer se meus dados não atenderem às premissas da ANOVA de um fator? Você pode transformar os dados, usando correções como a ANOVA de Welch ou aplicando alternativas não paramétricas como o teste de Kruskal-Wallis.

P5: Como interpreto os resultados da ANOVA de um fator? Relate o valor-p e o tamanho do efeito da análise. Se o valor-p for menor que o nível de significância pré-determinado (por exemplo, 0,05), há uma diferença significativa entre os grupos. Use testes post hoc para identificar diferenças específicas entre os grupos.

P6: Quais são alguns erros típicos a evitar na ANOVA de um fator? Alguns erros comuns incluem não verificar as premissas, interpretar resultados não significativos sem considerar o contexto ou o poder estatístico, usar testes post hoc incorretos e não considerar o tamanho do efeito e a significância prática.

P7: Quais são alguns testes alternativos à ANOVA de um fator? Testes alternativos incluem a ANOVA de Welch (para variâncias desiguais) e o teste de Kruskal-Wallis (uma alternativa não paramétrica).

P8: O que são testes post hoc, e quando devo usá-los? Testes post hoc são usados após um resultado significativo de ANOVA de um fator para identificar pares específicos de grupos com diferenças significativas em suas médias. Exemplos incluem o teste de Tukey HSD, Bonferroni e o teste de Scheffe.

P9: Como visualizo os resultados da ANOVA de um fator? Você pode criar gráficos de caixa ou gráficos de barras para visualizar as diferenças entre as médias dos grupos. Além disso, relate as estatísticas resumidas descritivas de cada grupo (por exemplo, média, desvio padrão).

P10: Posso usar ANOVA de um fator para apenas dois grupos? Embora tecnicamente possível, é mais comum usar um teste t para amostras independentes para comparar as médias de dois grupos, pois é especificamente projetado para esse propósito.

Perguntas Frequentes (FAQ)

P1: O que é ANOVA de um fator?

ANOVA de um fator é uma ferramenta estatística usada para testar as diferenças entre as médias de três ou mais grupos independentes. Ajuda a determinar se há uma diferença significativa entre as médias ou se as diferenças são devido a variação aleatória.

P2: Quais são as premissas da ANOVA de um fator?

As premissas da ANOVA de um fator são independência das observações, normalidade dos resíduos (erros) e homogeneidade das variâncias.

P3: Como verifico as premissas para a ANOVA de um fator?

Você pode verificar a normalidade usando histogramas, gráficos Q-Q ou testes como Shapiro-Wilk ou Kolmogorov-Smirnov. A homogeneidade das variâncias pode ser verificada usando os testes de Levene ou Bartlett.

P4: O que devo fazer se meus dados não atenderem às premissas da ANOVA de um fator?

Você pode transformar os dados, usando correções como a ANOVA de Welch ou aplicando alternativas não paramétricas como o teste de Kruskal-Wallis.

P5: Como interpreto os resultados da ANOVA de um fator?

Relate o valor-p e o tamanho do efeito da análise. Se o valor-p for menor que o nível de significância pré-determinado (por exemplo, 0,05), há uma diferença significativa entre os grupos. Use testes post hoc para identificar diferenças específicas entre os grupos.

P6: Quais são alguns erros típicos a evitar na ANOVA de um fator?

Alguns erros comuns incluem não verificar as premissas, interpretar resultados não significativos sem considerar o contexto ou o poder estatístico, usar testes post hoc incorretos e não considerar o tamanho do efeito e a significância prática.

P7: Quais são alguns testes alternativos à ANOVA de um fator?

Testes alternativos incluem a ANOVA de Welch (para variâncias desiguais) e o teste de Kruskal-Wallis (uma alternativa não paramétrica).

P8: O que são testes post hoc, e quando devo usá-los?

Testes post hoc são usados após um resultado significativo de ANOVA de um fator para identificar pares específicos de grupos com diferenças significativas em suas médias. Exemplos incluem o teste de Tukey HSD, Bonferroni e o teste de Scheffe.

P9: Como visualizo os resultados da ANOVA de um fator?

Você pode criar gráficos de caixa ou gráficos de barras para visualizar as diferenças entre as médias dos grupos. Além disso, relate as estatísticas resumidas descritivas de cada grupo (por exemplo, média, desvio padrão).

P10: Posso usar ANOVA de um fator para apenas dois grupos?

Embora tecnicamente possível, é mais comum usar um teste t para amostras independentes para comparar as médias de dois grupos, pois é especificamente projetado para esse propósito.